题目内容
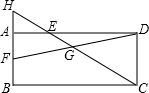如图，在矩形ABCD中，E、F分别是AD、AB边上的点，连接CE、DF，他们相交于点G，延长CE交BA的延长线于点H，则图中的相似三角形共有（ ）| A、5对 | B、4对 | C、3对 | D、2对 |
考点：相似三角形的判定
专题：
分析：根据相似三角形的判定定理进行解答即可．
解答：解：∵AD∥BC，
∴∠HAE=∠B，∠H=∠H，
∴△HAE∽△HBC；
∵∠AEH=∠DEC，AB∥CD，
∴∠DCE=∠HAE，
∴△HAE∽△CDE∽△HBC；
∵∠HGF=∠CDG，∠H=∠DCG，
∴△CDG∽△HFG，
∴图中的相似三角形共有4对．
故选B．
∴∠HAE=∠B，∠H=∠H，
∴△HAE∽△HBC；
∵∠AEH=∠DEC，AB∥CD，
∴∠DCE=∠HAE，
∴△HAE∽△CDE∽△HBC；
∵∠HGF=∠CDG，∠H=∠DCG，
∴△CDG∽△HFG，
∴图中的相似三角形共有4对．
故选B．
点评：本题考查的是相似三角形的判定，熟知有两组角对应相等的两个三角形相似是解答此题的关键．
练习册系列答案
金博士一点全通系列答案
相关题目
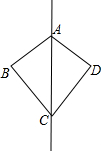如图，△ABC与△ADC关于AC所在的直线对称，∠BCD=70°，∠B=80°，则∠DAC的度数为（ ）| A、55° | B、65° |
| C、75° | D、85° |
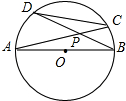如图，⊙O的直径AB=10，CD是⊙O的弦，AC与BD相交于点P．
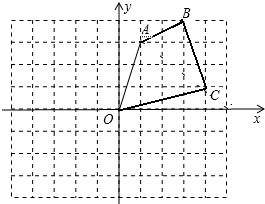在如图所示的边长均为1的正方形的方格纸中，建立直角坐标系，四边形OABC的位置如图所示．请将此四边形的各个顶点的横坐标不变，纵坐标分别乘-1，得到一个新图形，画出新的图形，并求出此图形的面积．