题目内容
 如图,要建一个面积为140平方米的仓库,仓库的一边靠墙,这堵墙的长为18米,在与墙垂直的一边要开一扇2米宽的门,已知围建仓库的现有木板材料可使新建板墙的总长为32米,那么这个仓库的宽和长分别为多少米?
如图,要建一个面积为140平方米的仓库,仓库的一边靠墙,这堵墙的长为18米,在与墙垂直的一边要开一扇2米宽的门,已知围建仓库的现有木板材料可使新建板墙的总长为32米,那么这个仓库的宽和长分别为多少米?考点:一元二次方程的应用
专题:几何图形问题
分析:首先设这个仓库的长为x米,则宽表示为
(32+2-x),再根据面积为140平方米的仓库可得x×
(32+2-x)=140,再解一元二次方程即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:设这个仓库的长为x米,由题意得:
x×
(32+2-x)=140,
解得:x1=20,x2=14,
∵这堵墙的长为18米,
∴x=20不合题意舍去,
∴x=14,
宽为:
×(32+2-14)=10(米).
答:这个仓库的宽和长分别为14米、10米.
x×
| 1 |
| 2 |
解得:x1=20,x2=14,
∵这堵墙的长为18米,
∴x=20不合题意舍去,
∴x=14,
宽为:
| 1 |
| 2 |
答:这个仓库的宽和长分别为14米、10米.
点评:此题主要考查了一元二次方程的应用,关键是正确理解题意,正确表示出长方形的长和宽.

练习册系列答案
相关题目
若等式
=
•
成立,则x的取值范围是( )
| x2-9 |
| x-3 |
| x+3 |
| A、x≥-3 | B、x≥3 |
| C、-3≤x≤3 | D、不能确定 |
 如图,下面不能判断是平行四边形的是( )
如图,下面不能判断是平行四边形的是( )| A、AB=CD,AD∥BC |
| B、AB∥CD,AD∥BC |
| C、AD=BC,AB=CD |
| D、∠B+∠DAB=180°,∠B+∠BCD=180° |
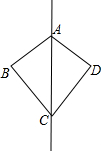 如图,△ABC与△ADC关于AC所在的直线对称,∠BCD=70°,∠B=80°,则∠DAC的度数为( )
如图,△ABC与△ADC关于AC所在的直线对称,∠BCD=70°,∠B=80°,则∠DAC的度数为( )| A、55° | B、65° |
| C、75° | D、85° |