题目内容
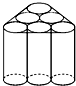 新学期开学,光明中学开展了一项名为“提倡节约,回收利用,从我做起”的活动.九年级(2)班李琼同学利用废旧的易拉罐制作了一个笔筒(罐与罐之间已用双面胶封紧),如图所示.为了美观,现欲将笔筒的侧面包上礼品纸,已知易拉罐的半径为r,高为h,则需礼品纸的面积为
新学期开学,光明中学开展了一项名为“提倡节约,回收利用,从我做起”的活动.九年级(2)班李琼同学利用废旧的易拉罐制作了一个笔筒(罐与罐之间已用双面胶封紧),如图所示.为了美观,现欲将笔筒的侧面包上礼品纸,已知易拉罐的半径为r,高为h,则需礼品纸的面积为考点:相切两圆的性质
专题:
分析:由题意可知笔筒的三个侧面面积相等,利用弧长公式和矩形的面积公即可求出需礼品纸的面积.
解答:解:如图所示: AB=(r+2r+r)=4r,
AB=(r+2r+r)=4r,
∴矩形ABCD的面积为4r×h=4rh,
∵∠C=120°,
∴L=
=
=
πr,
∴展开后的面积为
πrh,
∴三个侧面的面积=3×4rh+3×
πrh
=12rh+2πrh,
=2(π+6)rh,
故答案为:2(π+6)rh.
 AB=(r+2r+r)=4r,
AB=(r+2r+r)=4r,∴矩形ABCD的面积为4r×h=4rh,
∵∠C=120°,
∴L=
| nπr |
| 180 |
| 120×π×r |
| 180 |
| 2 |
| 3 |
∴展开后的面积为
| 2 |
| 3 |
∴三个侧面的面积=3×4rh+3×
| 2 |
| 3 |
=12rh+2πrh,
=2(π+6)rh,
故答案为:2(π+6)rh.
点评:本题考查了相切两圆的性质:如果两圆相切,那么连心线必经过切点,以及矩形的面积公式、弧长公式,解题的关键是把立体图形转化为我们熟悉的平面图形.

练习册系列答案
相关题目
某校初三•一班学生参加体育加试,第一小组引体向上的成绩如下表所示:
则这组学生引体向上个数的众数和中位数分别为( )
| 引体向上的个数 | 7 | 8 | 9 | 10 |
| 人数 | 2 | 1 | 4 | 5 |
| A、9.5和10 |
| B、9和10 |
| C、10和9.5 |
| D、10和9 |
已知两点A(1,2),B(3,1)到直线L的距离分别是
、
-
,则满足条件的直线L共有( )条.
| 2 |
| 5 |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
 如图,点C在⊙O上,若∠AOB=80°,则∠A+∠B=
如图,点C在⊙O上,若∠AOB=80°,则∠A+∠B=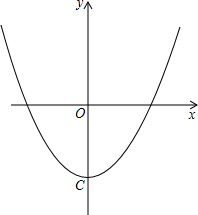 已知,一次函数y=x+m-2与二次函数y=x2-2的图象从左至右的交点依次为点B、A.
已知,一次函数y=x+m-2与二次函数y=x2-2的图象从左至右的交点依次为点B、A.