题目内容
如图，点C在⊙O上，若∠AOB=80°，则∠A+∠B=考点：圆周角定理
专题：
分析：首先连接AB，由圆周角定理，可求得∠C的度数，然后根据三角形的内角和定理，即可求得∠CAB+∠CBA与∠OAB+∠OBA值，继而求得答案．
解答：
解：连接AB，
∵∠AOB=80°，
∴∠C=
∠AOB=40°，
∴∠CAB+∠CBA=140°，
∵∠OAB+∠OBA=180°-∠AOB=100°，
∴∠CAO+∠ABO=∠CAB+∠CBA-（∠OAB+∠OBA）=140°-100°=40°．
故答案为：40°．
解：连接AB，∵∠AOB=80°，
∴∠C=
| 1 |
| 2 |
∴∠CAB+∠CBA=140°，
∵∠OAB+∠OBA=180°-∠AOB=100°，
∴∠CAO+∠ABO=∠CAB+∠CBA-（∠OAB+∠OBA）=140°-100°=40°．
故答案为：40°．
点评：此题考查了圆周角定理与三角形的内角和定理．此题难度不大，解题的关键是掌握在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半定理的应用．
练习册系列答案
相关题目
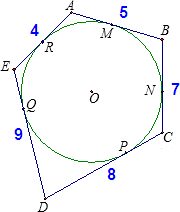如图，已知圆O内切于五边形ABCDE，切点分别是M、N、P、Q、R，且AB=5，BC=7，CD=8，DE=9，EA=4，则
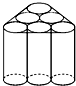新学期开学，光明中学开展了一项名为“提倡节约，回收利用，从我做起”的活动．九年级（2）班李琼同学利用废旧的易拉罐制作了一个笔筒（罐与罐之间已用双面胶封紧），如图所示．为了美观，现欲将笔筒的侧面包上礼品纸，已知易拉罐的半径为r，高为h，则需礼品纸的面积为已知|a|＞a，|b|＞b，且|a|＞|b|，则a、b的大小关系为（ ）
| A、a＞b | B、a=b |
| C、a＜b | D、无法确定 |