题目内容
已知两点A(1,2),B(3,1)到直线L的距离分别是
、
-
,则满足条件的直线L共有( )条.
| 2 |
| 5 |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
考点:圆与圆的位置关系
专题:
分析:根据题意,可以分别以A、B为圆心,以
,
-
为半径画圆,然后求两圆的公切线,公切线的条数就是直线l的条数.
| 2 |
| 5 |
| 2 |
解答:解:∵两点A(1,2),B(3,1),
∴|AB|=
,
分别以A,B为圆心,
,
-
为半径作两个圆,
则两圆外切,有三条公切线.
故选C.
∴|AB|=
| 5 |
分别以A,B为圆心,
| 2 |
| 5 |
| 2 |
则两圆外切,有三条公切线.
故选C.
点评:本题考查的是两点确定一条直线,题中求出的数据AB=
与点A、B到直线l的距离分别等于
,
-
起到了关键的限制作用,利用数形结合进行解答更形象直观.
| 5 |
| 2 |
| 5 |
| 2 |

练习册系列答案
相关题目
 ,则该汽车的车牌号码是
,则该汽车的车牌号码是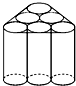 新学期开学,光明中学开展了一项名为“提倡节约,回收利用,从我做起”的活动.九年级(2)班李琼同学利用废旧的易拉罐制作了一个笔筒(罐与罐之间已用双面胶封紧),如图所示.为了美观,现欲将笔筒的侧面包上礼品纸,已知易拉罐的半径为r,高为h,则需礼品纸的面积为
新学期开学,光明中学开展了一项名为“提倡节约,回收利用,从我做起”的活动.九年级(2)班李琼同学利用废旧的易拉罐制作了一个笔筒(罐与罐之间已用双面胶封紧),如图所示.为了美观,现欲将笔筒的侧面包上礼品纸,已知易拉罐的半径为r,高为h,则需礼品纸的面积为