题目内容
1．
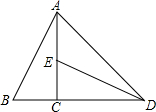如图所示，将Rt△ABC绕其直角顶点C按顺时针方向旋转90°后得到Rt△DEC，连接AD，若∠BAC=25°，则∠ADE=（ ）| A． | 20° | B． | 25° | C． | 30° | D． | 35° |
分析 根据旋转的性质可得AC=CD，∠CDE=∠BAC，再判断出△ACD是等腰直角三角形，然后根据等腰直角三角形的性质求出∠CAD=45°，根据∠ADE=∠CED-∠CAD．
解答 解：∵Rt△ABC绕其直角顶点C按顺时针方向旋转90°后得到Rt△DEC，
∴AC=CD，∠CDE=∠BAC=25°，
∴△ACD是等腰直角三角形，
∴∠CAD=45°，
∴∠ADE=∠CED-∠CAD=45°-25°=20°．
故选A．
点评 本题考查了旋转的性质，等腰直角三角形的判定与性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记各性质并准确识图是解题的关键．
练习册系列答案
相关题目
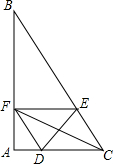如图，在△ABC中，∠A=90°，∠B=30°，AC=6cm，点D从点A开始以1cm/s的速度向点C运动，点E从点C开始以2cm/s的速度向点B运动，两点同时运动，同时停止，运动的时间为ts，过点E作EF∥AC交AB于点F．
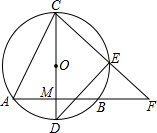如图，⊙O的弦AB=8，直径CD⊥AB于M，OM：MD=3：2，E是劣弧CB上一点，连结CE并延长交AB的延长线于点F，连结DE．