题目内容
17.在△ABC中.∠A=50°.AB,AC边上的高所在直线交于点H.则∠BHC的度数是140°或50°.分析 ①△ABC是锐角三角形时,先根据高线的定义求出∠ADB=90°,∠BEC=90°,然后根据直角三角形两锐角互余求出∠ABD,再根据三角形的一个外角等于与它不相邻的两个内角的和列式进行计算即可得解;②△ABC是钝角三角形时,根据直角三角形两锐角互余求出∠BHC=∠A,从而得解.
解答 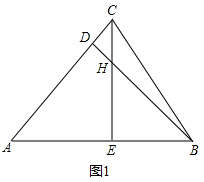 解:①如图1,△ABC是锐角三角形时,
解:①如图1,△ABC是锐角三角形时,
∵BD、CE是△ABC的高线,
∴∠ADB=90°,∠BEC=90°,
在△ABD中,∵∠A=50°,
∴∠ABD=90°-50°=40°,
∴∠BHC=∠ABD+∠BEC=50°+90°=140°;
②△ABC是钝角三角形时,∵BD、CE是△ABC的高线,
∴∠A+∠ACE=90°,∠BHC+∠HCD=90°,
∵∠ACE=∠HCD(对顶角相等),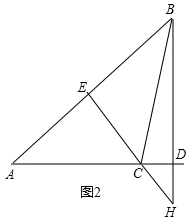
∴∠BHC=∠A=50°,
综上所述,∠BHC的度数是140°或50°,
故答案为:140°或50°.
点评 本题主要考查了三角形的内角和定理,三角形的高线,难点在于要分△ABC是锐角三角形与钝角三角形两种情况讨论,作出图形更形象直观.

练习册系列答案
相关题目
10.已知一组数据x1,x2,x3,x4,x5的平均数是2,方差是$\frac{1}{3}$,那么另一组数据3x1+1,3x2+1,3x3+1,3x4+1,3x5+1的平均数和方差分别是( )
| A. | 2,$\frac{1}{3}$ | B. | 2,1 | C. | 7,3 | D. | 3,3 |
12.为了了解某区八年级学生的体重情况,从中抽取了200名学生进行体重测试.在这个问欢迎登陆全品中考网“题中,下列说法错误的是( )
| A. | 200名学生的体重是一个样本 | B. | 200名是样本容量 | ||
| C. | 每个学生的体重是个体 | D. | 全县八年级学生的体重是总体 |
 如图,抛物线y=mx2-16mx+48m(m>0)与x轴交于A,B两点(点B在点A左侧),与y轴交于点C,点D是抛物线上的一个动点,且位于第四象限,连接OD、BD、AC、AD,延长AD交y轴于点E.
如图,抛物线y=mx2-16mx+48m(m>0)与x轴交于A,B两点(点B在点A左侧),与y轴交于点C,点D是抛物线上的一个动点,且位于第四象限,连接OD、BD、AC、AD,延长AD交y轴于点E.