Question

11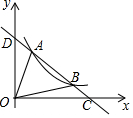．如图，一次函数y=kx+b与反比例函数y=$\frac{6}{x}$（x＞0）的图象交于A（m，6），B（3，n）两点，与x轴交于点C，与y轴交于点D，下列结论：①一次函数解析式为y=-2x+8；②AD=BC；③kx+b-$\frac{6}{x}$＜0的解集为0＜x＜1或x＞3；④△AOB的面积是8，其中正确结论的个数是（　　）

• A． 4个
• B． 3个
• C． 2个
• D． 1个

Answer 1

分析 根据双曲线解析式求得点A、B坐标，待定系数法可得直线解析式，即可判断①；由直线解析式求得C、D坐标，由两点间的距离公式求得AD、BC的长，即可判断②；由函数图象知直线在双曲线下方时x的范围即可判断③；利用割补法求得△AOB的面积即可判断④．

解答 解：（1）把点（m，6），B（3，n）分别代入y=$\frac{6}{x}$（x＞0）得m=1，n=2，
∴A点坐标为（1，6），B点坐标为（3，2），
把A（1，6），B（3，2）分别代入y=kx+b，
得$\left\{\begin{array}{l}{k+b=6}\\{3k+b=2}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=-2}\\{b=8}\end{array}\right.$，
∴一次函数解析式为y=-2x+8，故①正确；

在y=-2x+8中，当x=0时，y=8，即D（0，8），
当y=0时，-2x+8=0，解得：x=4，即C（4，0），
则AD=$\sqrt{（0-1）^{2}+（8-6）^{2}}$=$\sqrt{5}$，BC=$\sqrt{（4-3）^{2}+（0-2）^{2}}$=$\sqrt{5}$，
∴AD=BC，故②正确；

由函数图象知，直线在双曲线下方时x的范围是0＜x＜1或x＞3，
∴kx+b-$\frac{6}{x}$＜0的解集为0＜x＜1或x＞3，故③正确；

分别过点A、B作AE⊥x轴，BF⊥x轴，垂足分别是E、F点．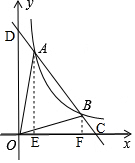

∵A（1，6），B（3，2），
∴AE=6，BF=2，
∴S_△AOB=S_△AOC-S_△BOC=$\frac{1}{2}$×4×6-$\frac{1}{2}$×4×2=8，故④正确；
故选：A．

点评 本题主要考查直线和双曲线交点的问题，熟练掌握待定系数法求函数解析式、两点间的距离公式、割补法求三角形的面积是解题的关键．