题目内容
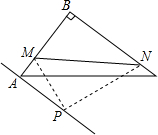 如图,在△ABC中,∠ABC=90°,AB=6,BC=8,点M、N分别在边AB、BC上,沿直线MN将△ABC折叠,点B落在点P处,如果AP∥BC且AP=4,那么BN=
如图,在△ABC中,∠ABC=90°,AB=6,BC=8,点M、N分别在边AB、BC上,沿直线MN将△ABC折叠,点B落在点P处,如果AP∥BC且AP=4,那么BN=考点:翻折变换(折叠问题),解直角三角形
专题:
分析:如图,证明∠MBO=∠BNO;求出BP、BO的长度;证明△ABP∽△OBN,列出比例式即可解决问题.
解答: 解:如图,连接BP,交MN于点O;
解:如图,连接BP,交MN于点O;
则BO=PO,BO⊥MN;
∵∠ABC=90°,
∴∠MBO+∠NBO=∠NBO+∠BNO,
∴∠MBO=∠BNO;
∵AP∥BC,且∠ABC=90°,
∴∠BAP=90°;
由勾股定理得:BP2=AB2+AP2,
∵AB=6,AP=4,
∴BP=2
,BO=
,
∵∠ABP=∠BNO,
∴△ABP∽△OBN,
∴
=
,解得:BN=
.
故答案为
.
 解:如图,连接BP,交MN于点O;
解:如图,连接BP,交MN于点O;则BO=PO,BO⊥MN;
∵∠ABC=90°,
∴∠MBO+∠NBO=∠NBO+∠BNO,
∴∠MBO=∠BNO;
∵AP∥BC,且∠ABC=90°,
∴∠BAP=90°;
由勾股定理得:BP2=AB2+AP2,
∵AB=6,AP=4,
∴BP=2
| 13 |
| 13 |
∵∠ABP=∠BNO,
∴△ABP∽△OBN,
∴
| AP |
| BO |
| PB |
| BN |
| 13 |
| 2 |
故答案为
| 13 |
| 2 |
点评:该题主要考查了翻折变换的性质及其应用问题;解题的关键是灵活运用勾股定理、相似三角形的判定及其性质等几何知识点来分析、判断、推理或解答.

练习册系列答案
相关题目
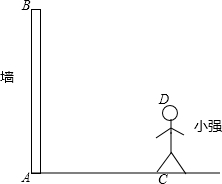 某一时刻身高为1.5m的小强CD在太阳光下的影长为2m,学校有一堵墙AB高为3m,如图所示,此刻小强行走在院墙内,若不想被太阳光照射到,请通过计算说明小强可以走动的范围.
某一时刻身高为1.5m的小强CD在太阳光下的影长为2m,学校有一堵墙AB高为3m,如图所示,此刻小强行走在院墙内,若不想被太阳光照射到,请通过计算说明小强可以走动的范围.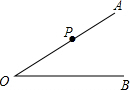 如图,已知∠AOB,P是射线OA上一点,按下列要求作图(保留作图痕迹,不要求写作法)
如图,已知∠AOB,P是射线OA上一点,按下列要求作图(保留作图痕迹,不要求写作法)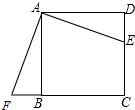 如图,在边长为6的正方形ABCD中,E是CD上一点,F在CB的延长线上,且DE=BF.
如图,在边长为6的正方形ABCD中,E是CD上一点,F在CB的延长线上,且DE=BF.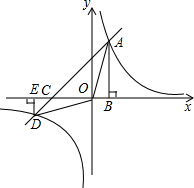 如图,已知Rt△ABC的顶点A是一次函数y=x+m与反比例函数y=
如图,已知Rt△ABC的顶点A是一次函数y=x+m与反比例函数y= 如图,请把△ABC和△A′B′C′图形补充完整,使得它们关于直线l对称.(保留作图痕迹)
如图,请把△ABC和△A′B′C′图形补充完整,使得它们关于直线l对称.(保留作图痕迹)