题目内容
11. 如图,已知A(-3,n),B(2,-3)是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,已知A(-3,n),B(2,-3)是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点.(1)写出一次函数和反比例函数的解析式y=-x-1,y=-$\frac{6}{x}$;
(2)观察图象,直接写出方程kx+b-$\frac{m}{x}$=0的解;
(3)观察图象,直接写出kx+b-$\frac{m}{x}$<0的解集;
(4)求△AOB的面积.
分析 (1)根据图象上的点满足函数解析式,可得点的坐标,根据待定系数法,可得一次函数的解析式;
(2)方程kx+b-$\frac{m}{x}$=0的解就是一次函数与反比例函数交点的横坐标;
(3)根据一次函数图象在反比例函数图象下方的部分是不等式的解集,可得答案;
(4)(2)根据三角形的面积公式,三角形面积的和差,可得答案.
解答 解:(1)B(2,-3)都在反比例函数y=$\frac{m}{x}$的图象上,
∴m=2×(-3)=-6,
则反比例函数的解析式是y=-$\frac{6}{x}$,
当x=-3时,y=n=2,
则A的坐标是(-3,2).
根据题意得$\left\{\begin{array}{l}{-3k+b=2}\\{2k+b=-3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=-1}\end{array}\right.$,
则一次函数的解析式是y=-x-1.
故答案是:y=-x-1,y=-$\frac{6}{x}$;
(2)根据题意得方程kx+b-$\frac{m}{x}$=0的解是x=-3或2;
(3)kx+b-$\frac{m}{x}$<0的解集是:-3<x<0或x>2;
(4)在y=-x-1中,令y=0,解得x=-1,
则C的坐标是(-1,0)
S△AOC=$\frac{1}{2}$×1×2=1,S△BOC=$\frac{1}{2}$×1×3=$\frac{3}{2}$,
S△AOB=S△AOC+S△BOC=1+$\frac{3}{2}$=$\frac{5}{2}$.
点评 本题考查了反比例函数与一次函数的交点问题,待定系数法求解析式,三角形面积公式及三角形面积的和差,利用函数图象与不等式的关系解不等式.

| A. | yx | B. | xy | C. | 10y+x | D. | 10x+y |
 已知一次函数y=kx+3(k<0)的图象与x轴、y轴分别相交于点A、B,tan∠OAB=2,点P(a,b)是在该函数的图象上的一点.
已知一次函数y=kx+3(k<0)的图象与x轴、y轴分别相交于点A、B,tan∠OAB=2,点P(a,b)是在该函数的图象上的一点. 已知AD⊥BC于D,EG⊥BC于G,∠E=∠3,AD平分∠BAC吗?若平分,请写出推理过程;若不平分,试说明理由.
已知AD⊥BC于D,EG⊥BC于G,∠E=∠3,AD平分∠BAC吗?若平分,请写出推理过程;若不平分,试说明理由.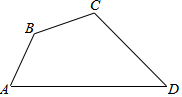 四边形ABCD中,AB=$\sqrt{6}$,BC=5-$\sqrt{3}$,CD=6,∠ABC=135°,∠BCD=120°,求AD的长.
四边形ABCD中,AB=$\sqrt{6}$,BC=5-$\sqrt{3}$,CD=6,∠ABC=135°,∠BCD=120°,求AD的长.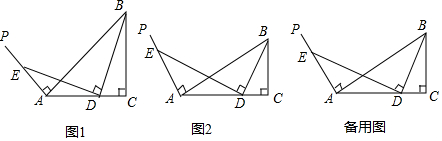
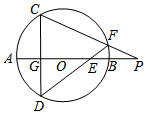 (如图)AB是⊙O的直径,弦CD⊥AB于点G,E是线段AB上一动点(不与点A、B、G重合),直线DE交⊙O于点F,直线CF交直线AB于点P,设⊙O的半径为r,求证:OE•OP=r2.
(如图)AB是⊙O的直径,弦CD⊥AB于点G,E是线段AB上一动点(不与点A、B、G重合),直线DE交⊙O于点F,直线CF交直线AB于点P,设⊙O的半径为r,求证:OE•OP=r2.