题目内容
已知:正方形ABCD的边长为2,P为正方形ABCD内一点,则PA+PB+PC的最小值为 .
考点:正弦定理与余弦定理
专题:
分析:顺时针旋转△BPC60°,可得△PBE为等边三角形,若PA+PB+PC=AP+PE+EF要使最小只要AP,PE,EF在一条直线上,求出AF的值即可.
解答: 解:顺时针旋转△BPC60度,可得△PBE为等边三角形.
解:顺时针旋转△BPC60度,可得△PBE为等边三角形.
即得PA+PB+PC=AP+PE+EF要使最小只要AP,PE,EF在一条直线上,
即如下图:可得最小PA+PB+PC=AF.
BM=BF•cos30°=BC•cos30°=
,
则AM=2+
,
∵AB=BF,∠ABF=150°
∴∠BAF=15°
既得AF=
=
+
.
即PA+PB+PC的最小值是
+
.
 解:顺时针旋转△BPC60度,可得△PBE为等边三角形.
解:顺时针旋转△BPC60度,可得△PBE为等边三角形.即得PA+PB+PC=AP+PE+EF要使最小只要AP,PE,EF在一条直线上,
即如下图:可得最小PA+PB+PC=AF.
BM=BF•cos30°=BC•cos30°=
| 3 |
则AM=2+
| 3 |
∵AB=BF,∠ABF=150°
∴∠BAF=15°
既得AF=
| AM |
| cos15° |
| 2 |
| 6 |
即PA+PB+PC的最小值是
| 2 |
| 6 |
点评:本题主要考查轴对称-路线最短问题,正弦定理与余弦定理.解答本题的关键是熟练掌握旋转的知识.

练习册系列答案
相关题目
小刘用84米长的铁丝围成一个长方形,要使长比宽多4米,则长方形的长为( )
| A、29 | B、27 | C、25 | D、23 |
 如图,是一个四边形的边角料,AD=3cm,AB=4cm,BC=12cm,CD=13cm,∠A=90°,求四边形ABCD的面积.
如图,是一个四边形的边角料,AD=3cm,AB=4cm,BC=12cm,CD=13cm,∠A=90°,求四边形ABCD的面积.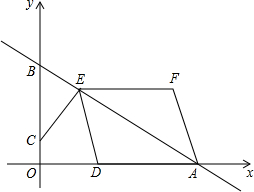 如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(4,0),B(0,3).点C的坐标为(0,m),过点C作CE⊥AB于点E,点D为x轴正半轴的一动点,且满足OD=2OC,连结DE,以DE,DA为边作?DEFA.
如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(4,0),B(0,3).点C的坐标为(0,m),过点C作CE⊥AB于点E,点D为x轴正半轴的一动点,且满足OD=2OC,连结DE,以DE,DA为边作?DEFA. 如图,将
如图,将
 如图,EF∥AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,则∠FEC=
如图,EF∥AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,则∠FEC=