题目内容
3.如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,5秒后,两点相距15个单位长度.已知点B的速度是点A的速度的2倍(速度单位:单位长度/秒).(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动5秒时的位置;

(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,再过几秒时,原点恰好处在点A、点B的正中间?
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从原点O位置出发向B点运动,且C的速度是点A的速度的一半;当C运动几秒后,C为AB的中点?
分析 (1)设A的速度是x,则B的速度为4x,根据行程问题的数量关系建立方程求出其解即可;
(2)设y秒后,原点恰好在A、B的正中间,根据两点到原点的距离相等建立方程求出其解即可;
(3)设当C运动z秒后,C为AB的中点,由中点坐标公式就可以求出结论.
解答 解:(1)设A的速度是x,则B的速度为2x,由题意,得
5(x+2x)=15,
解得:x=1,
∴B的速度为2,
∴A到达的位置为-5,B到达的位置是10,在数轴上的位置如图:
答:A的速度为1;B的速度为2.
(2)设y秒后,原点恰好在A、B的正中间,由题意,得
10-2y=y+5,
y=$\frac{5}{3}$.
答:再过$\frac{5}{3}$秒时,原点恰好处在点A、点B的正中间;
(3)设当C运动z秒后,C为AB的中点,由题意得
10-2z-$\frac{1}{2}$z=$\frac{1}{2}$(10-2z+5+z),
解得:z=1.25.
答:当C运动1.25秒后,C为AB的中点.
点评 本题考查了行程问题的数量关系的运用,相遇问题的数量关系的运用,列一元一次方程解实际问题的运用,数轴的运用,解答时由行程问题的数量关系建立方程是关键.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
11.观察下列各式数:-2x,4x2,-8x3,16x4,-32x5,…则第n个式子是( )
| A. | -2n-1xn | B. | (-2)n-1xn | C. | -2nxn | D. | (-2)nxn |
8.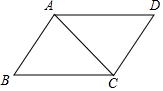 如图,已知AB∥CD,AD∥CB,则△ABC≌△CDA的依据是( )
如图,已知AB∥CD,AD∥CB,则△ABC≌△CDA的依据是( )
 如图,已知AB∥CD,AD∥CB,则△ABC≌△CDA的依据是( )
如图,已知AB∥CD,AD∥CB,则△ABC≌△CDA的依据是( )| A. | SAS | B. | ASA | C. | AAS | D. | SSS |
13.在-8,2.6,-3$\frac{1}{2}$,0,2$\frac{2}{3}$,-5.7中,负数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 5个 |


 如图,要设计一幅长为60cm,宽为40cm的矩形图案,其中有两横两竖的矩形彩条,横竖彩条宽度比为1:2,若彩条所占面积是图案面积的一半,求一条横彩条的宽度.
如图,要设计一幅长为60cm,宽为40cm的矩形图案,其中有两横两竖的矩形彩条,横竖彩条宽度比为1:2,若彩条所占面积是图案面积的一半,求一条横彩条的宽度.