题目内容
17．关于一次函数y=-2x+3，下列结论正确的是（ ）| A． | 图象过点（1，-1） | B． | 图象经过一、二、三象限 | ||
| C． | y随x的增大而增大 | D． | 函数图象与x轴交点坐标是（$\frac{3}{2}$，0） |
分析 A、把点的坐标代入关系式，检验是否成立；
B、根据系数的性质判断，或画出草图判断；
C、根据一次项系数判断；
D、可根据函数图象判断，亦可解不等式求解．
解答 解：A、当x=1时，y=1．所以图象不过（1，-1），故错误；
B、∵-2＜0，3＞0，
∴图象过一、二、四象限，故错误；
C、∵-2＜0，
∴y随x的增大而减小，故错误；
D、画出草图．
∵当x＞$\frac{3}{2}$时，图象在x轴下方，
∴y＜0，故正确．
故选D．
点评 本题主要考查了一次函数的性质以及一次函数与方程、不等式的关系．常采用数形结合的方法求解．
练习册系列答案
相关题目
数a，b，c在数轴上的位置如图所示，化简式子|a-b|-|b-c|-|a+c|-|b|+2|a|．
12．抛物线y=（x-2）2+4的顶点坐标是（ ）
| A． | （2，-4） | B． | （-2，4） | C． | （-2，-4） | D． | （2，4） |
2．下列几个命题中：
①|-5|的算术平方根是5；
②数据7、1、3、5、6、3的中位数是3，众数是4；
③对顶角相等；
④点P（1，-2）关于x轴的对称点在第三象限，
其中真命题的个数是（ ）
①|-5|的算术平方根是5；
②数据7、1、3、5、6、3的中位数是3，众数是4；
③对顶角相等；
④点P（1，-2）关于x轴的对称点在第三象限，
其中真命题的个数是（ ）
| A． | 3 | B． | 2 | C． | 1 | D． | 0 |
9．阅读：在直线上有n个不同的点，则此图中共有多少条线段？通过分析、画图尝试得如下表格：
问题：
（1）把表格补充完整；
（2）根据上述得到的信息解决下列问题：
①某学校七年级共有20个班进行辩论赛，规定进行单循环赛（每两班赛一场），那么该校七年级的辩论赛共要进行多少场？
②乘火车从A站出发，沿途经过10个车站方可到达B站，那么在A，B两站之间需要安排多少种不同的车票？
| 图形 | 直线上点的个数 | 共有线段的条数 | 两者关系 |
 | 2 | 1 | 0+1=$\frac{2×（2-1）}{2}$=1 |
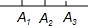 | 3 | 3 | 0+1+2=$\frac{3×（3-1）}{2}$=3 |
 | 4 | 6 | 0+1+2+3=$\frac{4×（4-1）}{2}$=6 |
| … | … | … | … |
 | n |
（1）把表格补充完整；
（2）根据上述得到的信息解决下列问题：
①某学校七年级共有20个班进行辩论赛，规定进行单循环赛（每两班赛一场），那么该校七年级的辩论赛共要进行多少场？
②乘火车从A站出发，沿途经过10个车站方可到达B站，那么在A，B两站之间需要安排多少种不同的车票？
已知二次函数y=ax2+bx+c的图象如图所示，它与x轴的两个交点的坐标分别为（-1，0），（3，0）．对于下列结论：①abc＞0，；b2-4ac＞0；③当x1＜x2＜0时，y1＞y2；④当-1＜x＜3时，y＞0．其中正确的有①②③个．