题目内容
如图,下列是由边长为2的等边三角形按照一定规律排列而成,第一个图形的周长为6,第二个所组成图形的周长为8,将若干的等边三角形按照这样的规律来摆放,则第8个图形的周长( )


| A、18 | B、19 | C、20 | D、21 |
考点:规律型:图形的变化类
专题:规律型
分析:观察图形得到第1个图形的周长为6,第2个所组成图形的周长为6+2,第3个图形的周长为6+2×2=10,即后面每个图形的周长比它前面的图形的周长多2,
由此得到第n个图形的周长为6+(n-1)×2,然后把n=8代入计算即可.
由此得到第n个图形的周长为6+(n-1)×2,然后把n=8代入计算即可.
解答:解:第1个图形的周长为6,
第2个所组成图形的周长为6+2,
第3个图形的周长为6+2×2=10,
第4个图形的周长为6+3×2=12,
所以第8个图形的周长为6+7×2=20.
故选C.
第2个所组成图形的周长为6+2,
第3个图形的周长为6+2×2=10,
第4个图形的周长为6+3×2=12,
所以第8个图形的周长为6+7×2=20.
故选C.
点评:本题考查了规律型:图形的变化类:通过从一些特殊的图形变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图,第①个图有2个相同的小正方形,第②个图有6个相同的小正方形,第③个图有12个相同的小正方形,…,按此规律,那么第15个图中小正方形的个数是( )
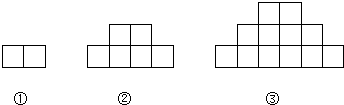

| A、225 | B、240 |
| C、30 | D、255 |
有甲、乙两块铁板(厚度忽略不计),甲的形状为直角梯形,两底边长分别为4cm,10cm,且有一内角为60°;乙的形状为等腰三角形,其顶角为45°,腰长12cm.在不改变形状的前提下,试图分别把它们从一个直径为8.7cm的圆洞中穿过,结果是( )
| A、甲板能穿过,乙板不能穿过 |
| B、甲板不能穿过,乙板能穿过 |
| C、甲、乙两板都能穿过 |
| D、甲、乙两板都不能穿过 |

 如图,与∠1是同位角的角是
如图,与∠1是同位角的角是 如图,一束光线与水平镜面的夹角为α,该光线先照射到平面镜上,然后在两个平面镜上反射.如果∠α=60°,∠β=50°,那么∠γ=
如图,一束光线与水平镜面的夹角为α,该光线先照射到平面镜上,然后在两个平面镜上反射.如果∠α=60°,∠β=50°,那么∠γ= 已知:AD∥BC,∠A=∠C.试说明∠1与∠2的关系.
已知:AD∥BC,∠A=∠C.试说明∠1与∠2的关系.