题目内容
13.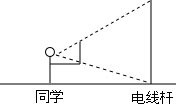 如图,某同学拿着一只有刻度的尺子,站在距电线杆30m的位置,把手臂向前伸直,把尺子竖直,看到尺子遮住电线杆时,尺子刻度为12cm,已知臂长60cm,电线杆的长为6m.
如图,某同学拿着一只有刻度的尺子,站在距电线杆30m的位置,把手臂向前伸直,把尺子竖直,看到尺子遮住电线杆时,尺子刻度为12cm,已知臂长60cm,电线杆的长为6m.
分析 先求出△ABC∽△AEF,再根据三角形对应高的比等于对应边的比,这样就可以求出电线杆EF的高.
解答  解:作AN⊥EF于N,交BC于M,
解:作AN⊥EF于N,交BC于M,
∵BC∥EF,
∴AM⊥BC于M,
∴△ABC∽△AEF,
∴$\frac{BC}{EF}$=$\frac{AM}{AN}$,
∵AM=0.6m,AN=30m,BC=0.12m,
∴EF=$\frac{BC•AN}{AM}$=$\frac{0.12×30}{0.6}$=6(m).
故答案为:6m.
点评 本题考查了相似三角形的应用:利用影长测量物体的高度;利用相似测量河的宽度;借助标杆或直尺测量物体的高度.找出几何图形上相应线段的长是解题的关键.

练习册系列答案
相关题目
3.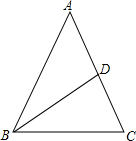 如图,在△ABC中,AB=AC,BD=BC,若∠A的度数为40°,则∠ABD等于( )
如图,在△ABC中,AB=AC,BD=BC,若∠A的度数为40°,则∠ABD等于( )
 如图,在△ABC中,AB=AC,BD=BC,若∠A的度数为40°,则∠ABD等于( )
如图,在△ABC中,AB=AC,BD=BC,若∠A的度数为40°,则∠ABD等于( )| A. | 70° | B. | 60° | C. | 50° | D. | 30° |
8.“十•一”黄金周期间,厦门鼓浪屿在7填中接待旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
若9月30日接待旅游人数记为a,
(1)请用a的代数式表示10月2日接待旅游的人数.
(2)若10月7日接待旅游人数为1.8万人,问9月30日接待旅游人数是多少万人?
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
| 人数变化 单位:万人 | +1.6 | +0.8 | -0.3 | -0.45 | 0.6 | +0.2 | -1.2 |
(1)请用a的代数式表示10月2日接待旅游的人数.
(2)若10月7日接待旅游人数为1.8万人,问9月30日接待旅游人数是多少万人?
5.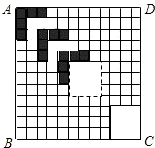 如图,正方形ABCD的边长为12,划分成12×12个小正方形格.将边长为n(n为整数,且2≤n≤11)的黑白两色正方形纸片按图中的方式黑白相间地摆放,第一张n×n的纸片正好盖住正方形ABCD左上角的n×n个小正方形格,第二张纸片盖住第一张纸片的部分恰好为(n-1)×(n-1)的正方形.如此摆放下去,最后直到纸片盖住正方形ABCD的右下角为止.
如图,正方形ABCD的边长为12,划分成12×12个小正方形格.将边长为n(n为整数,且2≤n≤11)的黑白两色正方形纸片按图中的方式黑白相间地摆放,第一张n×n的纸片正好盖住正方形ABCD左上角的n×n个小正方形格,第二张纸片盖住第一张纸片的部分恰好为(n-1)×(n-1)的正方形.如此摆放下去,最后直到纸片盖住正方形ABCD的右下角为止.
请你认真观察思考后回答下列问题:
(1)由于正方形纸片边长n的取值不同,完成摆放时所使用正方形纸片的张数也不同,请填写下表:
(2)设正方形ABCD被纸片盖住的面积(重合部分只计一次)为S1,未被盖住的面积为S2.
①当n=2时,求S1:S2的值;
②用含n的代数式表示S2.
 如图,正方形ABCD的边长为12,划分成12×12个小正方形格.将边长为n(n为整数,且2≤n≤11)的黑白两色正方形纸片按图中的方式黑白相间地摆放,第一张n×n的纸片正好盖住正方形ABCD左上角的n×n个小正方形格,第二张纸片盖住第一张纸片的部分恰好为(n-1)×(n-1)的正方形.如此摆放下去,最后直到纸片盖住正方形ABCD的右下角为止.
如图,正方形ABCD的边长为12,划分成12×12个小正方形格.将边长为n(n为整数,且2≤n≤11)的黑白两色正方形纸片按图中的方式黑白相间地摆放,第一张n×n的纸片正好盖住正方形ABCD左上角的n×n个小正方形格,第二张纸片盖住第一张纸片的部分恰好为(n-1)×(n-1)的正方形.如此摆放下去,最后直到纸片盖住正方形ABCD的右下角为止.请你认真观察思考后回答下列问题:
(1)由于正方形纸片边长n的取值不同,完成摆放时所使用正方形纸片的张数也不同,请填写下表:
| 纸片的边长n | 2 | 3 | 4 | 5 | 6 |
| 使用的纸片张数 | 11 | 10 | 9 | 8 | 7 |
①当n=2时,求S1:S2的值;
②用含n的代数式表示S2.
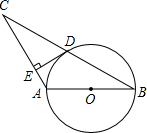 如图,△ABC中,AB=AC,且AB为⊙O的直径,⊙O交BC于点D,过D点作DE⊥AC于E
如图,△ABC中,AB=AC,且AB为⊙O的直径,⊙O交BC于点D,过D点作DE⊥AC于E