题目内容
3．
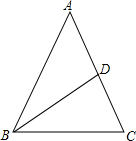如图，在△ABC中，AB=AC，BD=BC，若∠A的度数为40°，则∠ABD等于（ ）| A． | 70° | B． | 60° | C． | 50° | D． | 30° |
分析 根据等腰三角形两底角相等求出∠ABC=∠C，再求出∠CBD，然后根据∠ABD=∠ABC-∠CBD代入数据计算即可得解．
解答 解：∵AB=AC，∠A=40°，
∴∠ABC=∠C=$\frac{1}{2}$（180°-40°）=70°，
∵BD=BC，
∴∠CBD=180°-70°×2=40°，
∴∠ABD=∠ABC-∠CBD
=70°-40°
=30°．
故选D．
点评 本题考查了等腰三角形两底角相等的性质，三角形的内角和定理，熟记性质并准确识图是解题的关键．
练习册系列答案
相关题目
14．下列各式中，去括号正确的是（ ）
| A． | -（2x+y）=-2x+y | B． | 2（x-y）=2x-y | C． | 3x-（2y+z）=3x-2y-z | D． | x-（-y+z）=x-y-z |
11．比$\frac{1}{3}$的倒数小4的数是（ ）
| A． | -$\frac{11}{3}$ | B． | -1 | C． | 1 | D． | $\frac{11}{3}$ |
如图，已知在△ABC中，∠C=90°，AC＜BC，D为BC上一点，且到A、B两点的距离相等．
15．
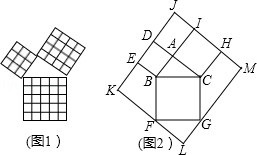勾股定理被誉为“几何明珠”，在数学的发展历程中占有举足轻重的地位．如图1是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理．图2是由图1放入长方形内得到的，∠BAC=90°，AB=3，AC=4，点D、E、F、G、H、I 都在长方形KLMJ的边上，则长方形KLMJ的面积为（ ）
勾股定理被誉为“几何明珠”，在数学的发展历程中占有举足轻重的地位．如图1是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理．图2是由图1放入长方形内得到的，∠BAC=90°，AB=3，AC=4，点D、E、F、G、H、I 都在长方形KLMJ的边上，则长方形KLMJ的面积为（ ）| A． | 90 | B． | 100 | C． | 110 | D． | 121 |
12．若x=1是方程x2+mx+n=0的一个根，则m+n-2等于（ ）
| A． | -7 | B． | 6 | C． | 1 | D． | -3 |
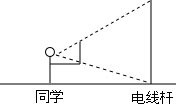如图，某同学拿着一只有刻度的尺子，站在距电线杆30m的位置，把手臂向前伸直，把尺子竖直，看到尺子遮住电线杆时，尺子刻度为12cm，已知臂长60cm，电线杆的长为6m．