题目内容
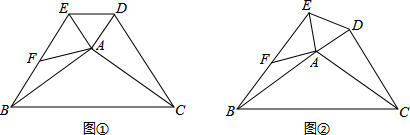
11.如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC+∠EAD=180°,△ABC不动,△ADE绕点A旋转,连接BE、CD,F为BE的中点,连接AF.(1)如图①,当∠BAE=90°时,求证:CD=2AF;
(2)当∠BAE≠90°时,(1)的结论是否成立?请结合图②说明理由;
(3)如图②,若∠ADC=90°,AD=5,AC=13,求BE2的值.
分析 (1)因为AF是直角三角形ABE的中线,所以BE=2AF,然后通过△ABE≌△ACD即可求得;
(2)延长EA交BC于G,在AG上截取AH=AD,证出△ABH≌△ACD从而证得BH=CD,然后根据三角形的中位线等于底边的一半,求得BH=2AF,即可求得;
(3)根据勾股定理求出CD,根据全等三角形的性质求出BH、EH,根据勾股定理计算即可.
解答 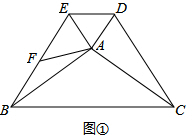 (1)证明:如图①,
(1)证明:如图①,
∵∠BAC+∠EAD=180°,∠BAE=90°,
∴∠DAC=90°,
在△ABE与△ACD中
$\left\{\begin{array}{l}{AE=AD}\\{∠BAE=∠CAD=90°}\\{AB=AC}\end{array}\right.$,
∴△ABE≌△ACD(SAS),
∴CD=BE,
∵在Rt△ABE中,F为BE的中点,
∴BE=2AF,
∴CD=2AF;
(2)成立,
证明:如图②,延长EA交BC于G,在AG上截取AH=AD,连接BH,
∵∠BAC+∠EAD=180°,
∴∠EAB+∠DAC=180°,
∵∠EAB+∠BAH=180°,
∴∠DAC=∠BAH,
在△ABH与△ACD中,
$\left\{\begin{array}{l}{AH=AD}\\{∠BAH=∠CAD}\\{AB=AC}\end{array}\right.$,
∴△ABH≌△ACD(SAS)
∴BH=DC,
∵AD=AE,AH=AD,
∴AE=AH,
∵EF=FB,
∴BH=2AF,
∴CD=2AF;
(3)∵∠ADC=90°,AD=5,AC=13,
∴CD2=AC2-AD2=144,
则CD=12,
由(2)得,BH=CD=12,EH=EA+AH=10,
∵△ABH≌△ACD,
∴∠BHE=∠ADC=90°,
∴BE2=BH2+EH2=244.
点评 本题考查了三角形全等的判定和性质,等腰三角形的性质,三角形中位线的性质等.作出正确的辅助线是解题关键.

 如图,正方形ABCD的对角线AC、BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M.
如图,正方形ABCD的对角线AC、BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M.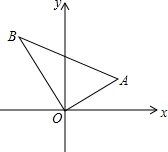 如图,Rt△ABO的顶点在原点,OA=12,AB=20,∠AOx=30°,求A,B两点的坐标,并求△AOB的面积.
如图,Rt△ABO的顶点在原点,OA=12,AB=20,∠AOx=30°,求A,B两点的坐标,并求△AOB的面积. 如图,在△ABC中,AD为内角平分线,∠ADC=60°,点E在AD上,满足DE=DB,射线CE交AB于点F.求证:AF•AB+CD•CB=AC2.
如图,在△ABC中,AD为内角平分线,∠ADC=60°,点E在AD上,满足DE=DB,射线CE交AB于点F.求证:AF•AB+CD•CB=AC2.