Question

9．△ABC外接圆的圆心为O，点P、Q分别在线段CA、AB上，K、L、M分别是BP、CQ、PQ的中点，圆O过K、L、M并且与PQ相切，证明：OP=OQ．

Answer 1

分析 如图，连接ML、MK、KL、OA、OC、OB、OP、OQ，作OG⊥AC于G，OH⊥AB于H．首先证明△APQ∽△MKL，推出$\frac{AP}{AQ}$=$\frac{MK}{ML}$=$\frac{BQ}{CP}$，推出AP•PC=AQ•QB，再证明OG²=OP²-PG²=OA²-AG²，OA²-OQ²=AQ•BQ，推出OA²-OP²=OA²-OQ²，由此即可解决问题．

解答 证明：如图，连接ML、MK、KL、OA、OC、OB、OP、OQ，作OG⊥AC于G，OH⊥AB于H．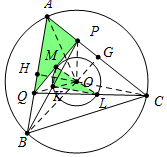

∵PM=MQ，PK=KB，
∴MK=$\frac{1}{2}$BQ，MK∥BQ，
∴∠AQP=∠QMK，
∵PQ是⊙O切线，
∴∠QMK=∠MLK，
∴∠AQP=∠MLK，
∵QM=MP，QL=LC，
∴ML=$\frac{1}{2}$PC，ML∥AC，
∴∠APQ=∠PML=∠MKL，
∴△APQ∽△MKL，
∴$\frac{AP}{AQ}$=$\frac{MK}{ML}$=$\frac{BQ}{CP}$，
∴AP•PC=AQ•QB，
∵OG⊥AC，OA=OC，
∴AG=GC，
∴OG²=OP²-PG²=OA²-AG²，
∴OA²-OP²=AG²-PG²=（AG+PG）（AG-PG）=PC•PA，
∵OH⊥AB，同理可得OA²-OQ²=AQ•BQ，
∴OA²-OP²=OA²-OQ²，
∴OP=OQ．

点评 本题考查切线的性质、三角形中位线定理、三角形外接圆、相似三角形的判定和性质、勾股定理、垂径定理等知识，解题的关键是学会添加常用辅助线，构造相似三角形解决问题，记住一些基本图形的基本结论，属于竞赛题目．