题目内容
6.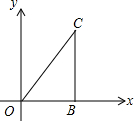 如图所示:在直角坐标系中,△OBC是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=$\sqrt{3}$,将△OBC绕原点O逆时针旋转60°得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°得到△OB2C2,…如此继续,得到△OB2016C2016则点C2016的坐标是(-2,0).
如图所示:在直角坐标系中,△OBC是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=$\sqrt{3}$,将△OBC绕原点O逆时针旋转60°得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°得到△OB2C2,…如此继续,得到△OB2016C2016则点C2016的坐标是(-2,0).
分析 先求出C1,C2,…C6的坐标,探究规律后即可解决问题.
解答 解:∵C(1,$\sqrt{3}$),C1(-1,$\sqrt{3}$),C2(-2,0),C3(-1,-$\sqrt{3}$),C4(1,-$\sqrt{3}$),C5(2,0),C6(1,$\sqrt{3}$)…,
∴从C6开始出现循环,
∴序号除以6整除的话坐标与C相同,余数是1坐标同C1,余数是2坐标同C2…,
∵2006÷6=334余2,
∴点C2016的坐标同C2,
∴点C2016的坐标(-2,0).
故答案为(-2,0).
点评 本题考查坐标与图形的变化-旋转、30度的直角三角形的性质等知识,解题的关键是从特殊到一般探究规律,发现规律,利用规律解决问题,属于中考常考题型.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
13.若点A(-5,y1),B(-3,y2),C(2,y3)在反比例函数y=$\frac{3}{x}$的图象上,则y1,y2,y3的大小关系是( )
| A. | y1<y3<y2 | B. | y1<y2<y3 | C. | y3<y2<y1 | D. | y2<y1<y3 |
10.$-\frac{1}{2016}$的相反数是( )
| A. | 2016 | B. | -2016 | C. | $\frac{1}{2016}$ | D. | $-\frac{1}{2016}$ |
11. 如图,OA、OB是⊙O的半径,C是⊙O上一点,∠ACB=20°,则∠OAB的度数为( )
如图,OA、OB是⊙O的半径,C是⊙O上一点,∠ACB=20°,则∠OAB的度数为( )
 如图,OA、OB是⊙O的半径,C是⊙O上一点,∠ACB=20°,则∠OAB的度数为( )
如图,OA、OB是⊙O的半径,C是⊙O上一点,∠ACB=20°,则∠OAB的度数为( )| A. | 80° | B. | 75° | C. | 70° | D. | 65° |
18.下列说法不正确的是( )
| A. | 选举中,人们通常最关心的数据是众数 | |
| B. | 从1,2,3,4,5中随机抽取一个数,取得奇数的可能性比较大 | |
| C. | 甲、乙两人在相同条件下各射击10次,他们的平均成绩相同,方差分别为S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定 | |
| D. | 数据3,5,4,1,-2的中位数是4 |
15.下列立体图形中,主视图是三角形的是( )
| A. |  | B. |  | C. |  | D. |  |
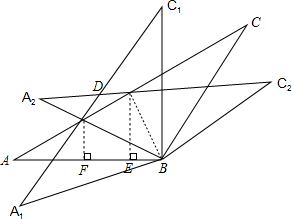 如图,在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B旋转30°得到△A1BC1,设AC交A1C1于点D,则点D到AB的距离为$\sqrt{3}$-1或1.
如图,在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B旋转30°得到△A1BC1,设AC交A1C1于点D,则点D到AB的距离为$\sqrt{3}$-1或1. 如图,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若∠A=∠D,CD=3,则图中阴影部分的面积为$\frac{3\sqrt{3}-π}{2}$.
如图,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若∠A=∠D,CD=3,则图中阴影部分的面积为$\frac{3\sqrt{3}-π}{2}$.