题目内容
15.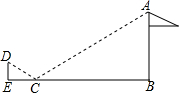 如图,为了测量旗杆AB的高度,小凡在距旗杆底部B点10.8米的C点处放置了一面镜子,当小凡行走到与BC位于同一直线的E点处时,恰好能从镜子中观察到旗杆顶部的A点.已知小凡眼睛所在的D点离地面的高度是1.6米,CE=2.7米,则旗杆AB的高度是( )
如图,为了测量旗杆AB的高度,小凡在距旗杆底部B点10.8米的C点处放置了一面镜子,当小凡行走到与BC位于同一直线的E点处时,恰好能从镜子中观察到旗杆顶部的A点.已知小凡眼睛所在的D点离地面的高度是1.6米,CE=2.7米,则旗杆AB的高度是( )| A. | 6.4米 | B. | 7.2米 | C. | 8米 | D. | 9.6米 |
分析 过点E作镜面的法线CH,由入射角等于反射角可知∠DCH=∠ACH,进而可得出∠ECD=∠BCA,由相似三角形的判定定理可得出△CDE∽△CAB,再根据相似三角形的对应边成比例即可求出AB的长.
解答 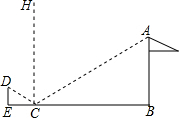 解:过点C作镜面的法线CH,由光学原理得∠DCH=∠ACH,
解:过点C作镜面的法线CH,由光学原理得∠DCH=∠ACH,
∵∠DCE=90°-∠DCH,
∠ACB=90°-∠ACH,
∴∠DCE=∠ACB,
又∵∠DEC=∠ABC=90°,
∴△CDE∽△CAB,
∴$\frac{DE}{AB}$=$\frac{CE}{CB}$,
即$\frac{1.6}{AB}$=$\frac{2.7}{10.8}$,
解得AB=6.4(m).
答:旗杆AB高为6.4米.
故选:A.
点评 本题考查的是相似三角形在实际生活中的应用,根据题意得出△CDE∽△CAB是解答此题的关键.

练习册系列答案
相关题目
10.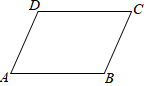 如图,AD=BC,要使四边形ABCD是平行四边形,还需补充的一个条件,下列错误的是( )
如图,AD=BC,要使四边形ABCD是平行四边形,还需补充的一个条件,下列错误的是( )
 如图,AD=BC,要使四边形ABCD是平行四边形,还需补充的一个条件,下列错误的是( )
如图,AD=BC,要使四边形ABCD是平行四边形,还需补充的一个条件,下列错误的是( )| A. | AB=DC | B. | AD∥BC | C. | ∠A+∠B=180° | D. | ∠A+∠D=180° |
4.用配方法解方程x2-8x+15=0时,下列变形中,正确的是( )
| A. | (x-4)2=31 | B. | (x-4)2=1 | C. | (x-8)2=1 | D. | (x-8)2=31 |
 在平面直角坐标系中,△ABO的三个顶点坐标分别为:A(2,3)、B(3,1)、O(0,0).
在平面直角坐标系中,△ABO的三个顶点坐标分别为:A(2,3)、B(3,1)、O(0,0).