题目内容
3. 在平面直角坐标系中,△ABO的三个顶点坐标分别为:A(2,3)、B(3,1)、O(0,0).
在平面直角坐标系中,△ABO的三个顶点坐标分别为:A(2,3)、B(3,1)、O(0,0).(1)将△ABO向左平移4个单位,画出平移后的△A1B1O1.
(2)将点O为对称中心,画出与△ABO成中心对称的△A2B2O.此时四边形ABA2B2的形状是平行四边形.
(3)在平面上是否存在点D,使得以A、B、O、D为顶点的四边形是平行四边形,若存在请直接写出符合条件的所有点的坐标;若不存在,请说明理由.
分析 (1)直接利用平移的性质得出对应点位置进而得出答案;
(2)直接利用旋转的性质结合平行四边形的判定方法得出答案;
(3)直接利用平行四边形的判定方法得出符合题意的答案.
解答  解:(1)△A1B1O1,即为所求;
解:(1)△A1B1O1,即为所求;
(2)△A2B2O,即为所求,此时四边形ABA2B2的形状是平行四边形;
故答案为:平行四边形;
(3)如图所示:D1(-1,2);D2(1,-2);D3(5,4)都是符合题意的点.
点评 此题主要考查了平移变换、旋转变换,正确得出对应点位置是解题关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
13.如图直线PQ、射线AB、线段MN能相交的是( )
| A. |  | B. |  | C. |  | D. |  |
11.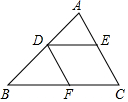 如图,DE∥BC,DF∥AC,则下列比例式中正确的是( )
如图,DE∥BC,DF∥AC,则下列比例式中正确的是( )
 如图,DE∥BC,DF∥AC,则下列比例式中正确的是( )
如图,DE∥BC,DF∥AC,则下列比例式中正确的是( )| A. | $\frac{AD}{DB}=\frac{DE}{BC}$ | B. | $\frac{AE}{EC}=\frac{BF}{FC}$ | C. | $\frac{DF}{AC}=\frac{DE}{BC}$ | D. | $\frac{EC}{AC}=\frac{BF}{BC}$ |
 如图,平行四边形ABCD中,对角线AC,BD交于O,EO⊥AC,
如图,平行四边形ABCD中,对角线AC,BD交于O,EO⊥AC,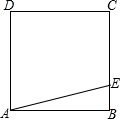 有一块边长为40米的正方形绿地ABCD,如图所示,在绿地旁边E处有健身器材,BE=9米.由于居住在A处的居民去健身践踏了绿地,小明想在A处树立一个标牌“少走■米,踏之何忍”.请你计算后帮小明在标牌的■处填上适当的数.
有一块边长为40米的正方形绿地ABCD,如图所示,在绿地旁边E处有健身器材,BE=9米.由于居住在A处的居民去健身践踏了绿地,小明想在A处树立一个标牌“少走■米,踏之何忍”.请你计算后帮小明在标牌的■处填上适当的数.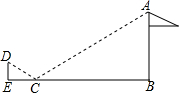 如图,为了测量旗杆AB的高度,小凡在距旗杆底部B点10.8米的C点处放置了一面镜子,当小凡行走到与BC位于同一直线的E点处时,恰好能从镜子中观察到旗杆顶部的A点.已知小凡眼睛所在的D点离地面的高度是1.6米,CE=2.7米,则旗杆AB的高度是( )
如图,为了测量旗杆AB的高度,小凡在距旗杆底部B点10.8米的C点处放置了一面镜子,当小凡行走到与BC位于同一直线的E点处时,恰好能从镜子中观察到旗杆顶部的A点.已知小凡眼睛所在的D点离地面的高度是1.6米,CE=2.7米,则旗杆AB的高度是( )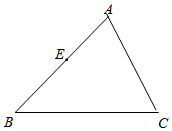 已知:如图,在△ABC中,过点A作AD⊥BC,垂足为D,E为AB上一点,过点E作EF⊥BC,垂足为F,过点D作DG∥AB交AC于点G.
已知:如图,在△ABC中,过点A作AD⊥BC,垂足为D,E为AB上一点,过点E作EF⊥BC,垂足为F,过点D作DG∥AB交AC于点G.