题目内容
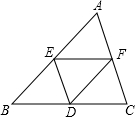 如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,如果△ABC的周长为20,那么△DEF的周长是( )
如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,如果△ABC的周长为20,那么△DEF的周长是( )| A、5 | B、10 | C、15 | D、20 |
考点:三角形中位线定理
专题:
分析:利用三角形的中位线定理可以得到:DE=
AC,EF=
BC,DF=
AB,则△DEF的周长是△ABC的周长的一半,据此即可求解.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵D、E分别是△ABC的边BC、AB的中点,
∴DE=
AC,
同理 EF=
BC,DF=
AB,
∴∴C△DEF=DE+EF+DF=
(AC+BC+AB)=
×20=10.
故选:B.
∴DE=
| 1 |
| 2 |
同理 EF=
| 1 |
| 2 |
| 1 |
| 2 |
∴∴C△DEF=DE+EF+DF=
| 1 |
| 2 |
| 1 |
| 2 |
故选:B.
点评:本题考查了三角形的中位线定理,正确根据三角形中位线定理证得:△DEF的周长是△ABC的周长的一半是关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 含有30°角的三角板如图放置在平面内,若三角板的最长边与直线m平行,则∠α的度数为( )
含有30°角的三角板如图放置在平面内,若三角板的最长边与直线m平行,则∠α的度数为( )| A、30° | B、45° |
| C、60° | D、90° |
若a>b,则下列结论中正确的是( )
| A、4a<4 b |
| B、a+c>b+c |
| C、a-5<b-5 |
| D、-7a>-7b |
下列计算,正确的是( )
| A、a6÷a2=a3 |
| B、3a2×2a2=6a2 |
| C、(ab2)2=a2b4 |
| D、5a+3a=8a2 |
 如图,直线a∥b,c是截线.若∠2=4∠1,则∠1的度数为( )
如图,直线a∥b,c是截线.若∠2=4∠1,则∠1的度数为( )| A、30° | B、36° |
| C、40° | D、45° |
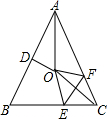 如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与线段AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是( )
如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与线段AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是( )| A、45° | B、50° |
| C、55° | D、60° |
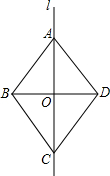 如图,直线l是四边形ABCD的对称轴.若AD∥BC,则下列结论:
如图,直线l是四边形ABCD的对称轴.若AD∥BC,则下列结论: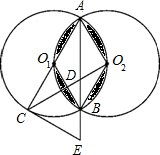 如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心,顺次连接A、O1、B、O2.
如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心,顺次连接A、O1、B、O2.