题目内容
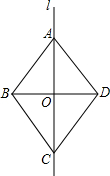 如图,直线l是四边形ABCD的对称轴.若AD∥BC,则下列结论:
如图,直线l是四边形ABCD的对称轴.若AD∥BC,则下列结论:(1)AB∥CD;(2)AB=BC;(3)BD平分∠ABC;(4)AO=CO.
其中正确的有
考点:轴对称的性质
专题:
分析:根据轴对称的性质可得∠1=∠2,∠3=∠4,根据两直线平行,内错角相等可得∠2=∠3,从而得到∠1=∠3=∠4,然后根据内错角相等,两直线平行可得AB∥CD,等角对等边可得AB=BC,再根据等腰三角形三线合一的性质可得BD平分∠ABC,AO=CO.
解答: 解:如图,∵直线l是四边形ABCD的对称轴,
解:如图,∵直线l是四边形ABCD的对称轴,
∴∠1=∠2,∠3=∠4,
∵AD∥BC,
∴∠2=∠3,
∴∠1=∠3=∠4,
∴AB∥CD,AB=BC,故(1)(2)正确;
由轴对称的性质,AC⊥BD,
∴BD平分∠ABC,AO=CO(等腰三角形三线合一),故(3)(4)正确.
综上所述,正确的是(1)(2)(3)(4).
故答案为:(1)(2)(3)(4).
 解:如图,∵直线l是四边形ABCD的对称轴,
解:如图,∵直线l是四边形ABCD的对称轴,∴∠1=∠2,∠3=∠4,
∵AD∥BC,
∴∠2=∠3,
∴∠1=∠3=∠4,
∴AB∥CD,AB=BC,故(1)(2)正确;
由轴对称的性质,AC⊥BD,
∴BD平分∠ABC,AO=CO(等腰三角形三线合一),故(3)(4)正确.
综上所述,正确的是(1)(2)(3)(4).
故答案为:(1)(2)(3)(4).
点评:本题考查了轴对称的性质,平行线的性质以及等腰三角形三线合一的性质,熟记各性质是解题的关键,用阿拉伯数字加弧线表示角更形象直观.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
微电子技术的不断进步,使半导体材料的加工尺寸大幅度缩小.某种电子元件的面积大约为0.000 000 71平方毫米,将0.000 000 71写成科学记数法表示为( )
| A、0.71×10-8 |
| B、7.1×10-6 |
| C、7.1×10-7 |
| D、7.1×10-8 |
下列运算正确的是( )
| A、x2•x3=x6 |
| B、(-x3)2=x6 |
| C、6x6÷2x2=3x3 |
| D、(x+y)2=x2+y2 |
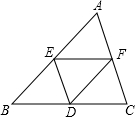 如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,如果△ABC的周长为20,那么△DEF的周长是( )
如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,如果△ABC的周长为20,那么△DEF的周长是( )| A、5 | B、10 | C、15 | D、20 |
 看图填空:
看图填空: 如图,有一小球在如图所示的地板上面自由滚动,则小球在地板上最终停留在黑色区域的概率为
如图,有一小球在如图所示的地板上面自由滚动,则小球在地板上最终停留在黑色区域的概率为 如图,把一张长方形纸条ABCD沿EF折叠,若∠1=56°,则∠EGF应为
如图,把一张长方形纸条ABCD沿EF折叠,若∠1=56°,则∠EGF应为 如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交BC的延长线于F,BG⊥AE于C,BG=4
如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交BC的延长线于F,BG⊥AE于C,BG=4