题目内容
先阅读材料,再根据所学方法解答下列问题:
我们在求1+2+3+…+99+100的值时,可以用下面的方法;
我们设S=1+2+3+…+99+100 ①,那么,S=100+99+98+…+3+2+1 ②;
然后,我们把①+②得:2S=(100+1)+(99+2)+(98+3)+…+(99+2)+(100+1),共100个101.
2S=101+101+101+…+101=100×101;
S=100×101÷2=5050.
亲爱的同学们,根据以上所学方法,聪明的你能解下面的题吗?当然,你会用其它方法解答也是正确的呀!请写出必要的步骤,否则不给分呀!
(1)1+3+5+…+97+99;
(2)5+10+15+…+195+200.
我们在求1+2+3+…+99+100的值时,可以用下面的方法;
我们设S=1+2+3+…+99+100 ①,那么,S=100+99+98+…+3+2+1 ②;
然后,我们把①+②得:2S=(100+1)+(99+2)+(98+3)+…+(99+2)+(100+1),共100个101.
2S=101+101+101+…+101=100×101;
S=100×101÷2=5050.
亲爱的同学们,根据以上所学方法,聪明的你能解下面的题吗?当然,你会用其它方法解答也是正确的呀!请写出必要的步骤,否则不给分呀!
(1)1+3+5+…+97+99;
(2)5+10+15+…+195+200.
考点:有理数的加法
专题:阅读型
分析:仿照材料的形式先计算2S的值然后求S的值即可.
解答:解:(1)设S=1+3+5+…+97+99①,那么S=99+97+…+5+3+1②,
①+②得:2S=(1+99)+(3+97)+…+(97+3)+(99+1),共50个100.
2S=100+100+…+100=50×100,
所以:S=2500,
即1+3+5+…+97+99=2500;
(2)设S=5+10+15+…+195+200①,那么S=200+195+…+15+10+5②,
①+②得:2S=(5+200)+(10+195)+(15+190)+…+(195+10)+(200+5),共20个205,
2S=205+205+…+205=205×20,
所以S=2050.
①+②得:2S=(1+99)+(3+97)+…+(97+3)+(99+1),共50个100.
2S=100+100+…+100=50×100,
所以:S=2500,
即1+3+5+…+97+99=2500;
(2)设S=5+10+15+…+195+200①,那么S=200+195+…+15+10+5②,
①+②得:2S=(5+200)+(10+195)+(15+190)+…+(195+10)+(200+5),共20个205,
2S=205+205+…+205=205×20,
所以S=2050.
点评:此题考查了有理数的加法,解题的关键是:表示2S的形式.

练习册系列答案
相关题目
下列运算正确的是( )
A、2
| ||||||
B、(-
| ||||||
C、
| ||||||
D、
|
下列说法错误的是( )
| A、1的平方根是1 | ||||
B、绝对值等于
| ||||
C、
| ||||
D、-3是
|
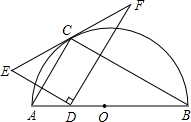 如图,点C在以AB为直径的半圆上,AB=10,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F,当点D从点A运动到点B时,线段EF扫过的面积是
如图,点C在以AB为直径的半圆上,AB=10,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F,当点D从点A运动到点B时,线段EF扫过的面积是