题目内容
用配方法解方程:3x2+4x-2=0.
考点:解一元二次方程-配方法
专题:
分析:解题时要注意解题步骤的准确使用,把左边配成完全平方式,右边化为常数.
解答:解:由原方程,得
x2+
x=
,
x2+
x+(
)2=
+(
)2,
(x+
)2=
,
x+
=±
,
解得 x1=
,x2=
.
x2+
| 4 |
| 3 |
| 2 |
| 3 |
x2+
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
(x+
| 2 |
| 3 |
| 10 |
| 9 |
x+
| 2 |
| 3 |
| ||
| 3 |
解得 x1=
-2+
| ||
| 3 |
-2-
| ||
| 3 |
点评:本题考查了解一元二次方程--配方法.配方法的一般步骤:
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方.
选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方.
选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 如图,在△ABC中,点D是AC上一点,添加下列哪个条件不能得到△CBD∽△CAB的是( )
如图,在△ABC中,点D是AC上一点,添加下列哪个条件不能得到△CBD∽△CAB的是( )| A、∠CDB=∠CBA |
| B、∠CBD=∠A |
| C、BC•AB=BD•AC |
| D、BC2=CD•AC |
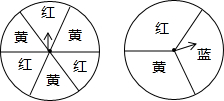 如图,用两个转盘进行“配绿色”游戏(黄色和蓝色配在一起为绿色),同时转动两个转盘,当转盘停止转动时,用两盘指针所指的颜色配色,求能配出绿色的概率(用树形图或列表法表示).
如图,用两个转盘进行“配绿色”游戏(黄色和蓝色配在一起为绿色),同时转动两个转盘,当转盘停止转动时,用两盘指针所指的颜色配色,求能配出绿色的概率(用树形图或列表法表示).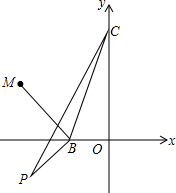 如图,已知,B(-1,0)、C(0,3)、P(-2,-1),M(-2.5,1.5),若点N在坐标平面内,满足△BMN∽△BPC,请直接写出所有符合条件的点N的坐标.
如图,已知,B(-1,0)、C(0,3)、P(-2,-1),M(-2.5,1.5),若点N在坐标平面内,满足△BMN∽△BPC,请直接写出所有符合条件的点N的坐标.