题目内容
15.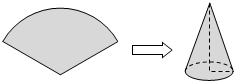 如图,用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥形无底纸帽(接缝忽略不计),则这个纸帽的高是( )
如图,用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥形无底纸帽(接缝忽略不计),则这个纸帽的高是( )| A. | $\sqrt{2}$cm | B. | 2$\sqrt{2}$cm | C. | 3$\sqrt{2}$cm | D. | 4$\sqrt{2}$cm |
分析 先利用弧长公式得到圆心角为120°,半径为6cm的扇形的弧长=4π,根据圆锥的侧面展开图为扇形,扇形的弧长等于圆锥的底面圆的周长,则可计算出圆锥的底面圆的半径为2,然后根据勾股定理可计算出圆锥的高.
解答 解:∵圆心角为120°,半径为6cm的扇形的弧长=$\frac{120π×6}{180}$=4π,
∴圆锥的底面圆的周长为4π,
∴圆锥的底面圆的半径为2,
∴这个纸帽的高=$\sqrt{{6}^{2}-{2}^{2}}$=4$\sqrt{2}$(cm).
故选D.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为扇形,扇形的弧长等于圆锥的底面圆的周长,扇形的半径等于圆锥的母线长.也考查了弧长公式和勾股定理.

练习册系列答案
相关题目
5.为了美化城市,建设中的某休闲广场准备用边长相同的正三角形与正方形两种地转镶嵌地面,在每一个顶点的周围,正三角形、正方形地转的个数分别是( )
| A. | 3,2 | B. | 2,3 | C. | 4,1 | D. | 2、2 |
6.若计算(x-5)(x+a)的结果是x2-bx-10,则a的值是( )
| A. | -2 | B. | 2 | C. | 3 | D. | -3 |
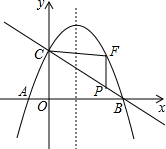 如图,已知抛物线y=ax2+bx+3与x轴交于A、B两点,与y轴交于点C,点A的坐标为(-1,0),对称轴为直线x=1,点P为线段BC上(不含B、C两点)的一个动点,PF∥y轴交抛物线于点F,设点P的横坐标为m.
如图,已知抛物线y=ax2+bx+3与x轴交于A、B两点,与y轴交于点C,点A的坐标为(-1,0),对称轴为直线x=1,点P为线段BC上(不含B、C两点)的一个动点,PF∥y轴交抛物线于点F,设点P的横坐标为m.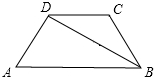 如图,在四边形ABCD中,DC∥AB,对角线BD平分∠ABC,且BD⊥AD,若AD=2,CD=3,则对角线BD的长为4$\sqrt{2}$.
如图,在四边形ABCD中,DC∥AB,对角线BD平分∠ABC,且BD⊥AD,若AD=2,CD=3,则对角线BD的长为4$\sqrt{2}$. 如图,?ABCD中,AE∥CF,AE与BC相交于点P,CF与BD相交于点Q,BP与DQ是否相等,请说明理由.
如图,?ABCD中,AE∥CF,AE与BC相交于点P,CF与BD相交于点Q,BP与DQ是否相等,请说明理由. 已知AB为⊙O的直径,弦BE=DE,AD,BE的延长线交于点C,求证:AC=AB.
已知AB为⊙O的直径,弦BE=DE,AD,BE的延长线交于点C,求证:AC=AB.