题目内容
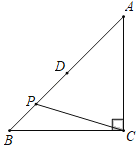
【题目】已知△ABC，∠ACB＝90°，AC＝BC＝4.D是AB的中点，P是平面上的一点，且DP＝1，连接BP、CP，将点B绕点P顺时针旋转90°得到点B′，连CB′，CB′的最大值是_____.
【答案】5
.
【解析】
如图，延长CD到N，DN＝CD，连接BN，NB′，CB′.利用相似三角形的性质求出NB′，根据CB′≤CN+NB′求解即可
解：如图，延长CD到N，DN＝CD，连接BN，NB′，CB′.
∴CA＝CB，∠ACB＝90°，BD＝AD，
∴CD⊥AB，
∵DN＝CD，
∴BN＝BC＝4，
∴∠CBD＝∠DBN＝45°，
∴∠CBN＝90°，
∴CN＝BC＝4，
∵BB′＝BP，BN＝BD，∠B′BP＝∠NBD＝45°，
∴
＝
＝，∠NBB′＝∠PBD，
∴△NBB′∽△DBP，
∴
＝＝，
∵PD＝1，
∴NB′＝，
∵CB′≤NB′+CN＝+4，
∴CB′≤5，
故答案为5.
练习册系列答案
阅读快车系列答案
相关题目
