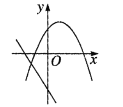题目内容
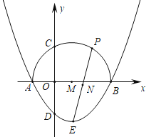
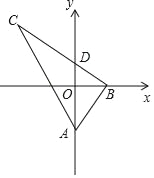
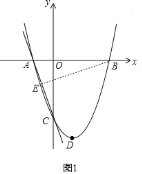
【题目】如图，抛物线y＝ax2﹣2ax+c的图象经过点C（0，﹣2），顶点D的坐标为（1，﹣
），与x轴交于A、B两点．
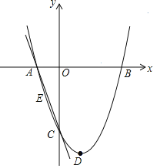
（1）求抛物线的解析式．
（2）连接AC，E为直线AC上一点，当△AOC∽△AEB时，求点E的坐标和
的值．
（3）点C关于x轴的对称点为H，当
FC+BF取最小值时，在抛物线的对称轴上是否存在点Q，使△QHF是直角三角形？若存在，请求出点Q的坐标；若不存在，请说明理由．
【答案】（1）
；
（2）E（﹣
，﹣
）；
；
（3）（1，
）或（1，
）或Q（1，2）或Q（1，﹣
）．
【解析】
（1）将点C、D的坐标代入抛物线表达式，即可求解；
（2）当△AOC∽△AEB时，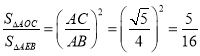
求出yE=-，由△AOC∽△AEB得：
即可求解；
（3）如图2，连接BF，过点F作FG⊥AC于G，当折线段BFG与BE重合时，CF+BF取得最小值，①当点Q为直角顶点时，由Rt△QHM∽Rt△FQM得：QM2=HMFM；②当点H为直角顶点时，点H（0，2），则点Q（1，2）；③当点F为直角顶点时，同理可得：点Q（1，-）．
（1）由题可列方程组：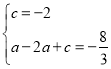
，解得：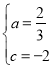
∴抛物线解析式为：y＝
x2﹣
x﹣2；
（2）由题意和勾股定理得，∠AOC＝90°，AC＝
，AB＝4，
设直线AC的解析式为：y＝kx+b，则
，
解得：
，
∴直线
当△AOC∽△AEB时
＝（
）2＝（
）2＝
，
∵S△AOC＝1，
∴S△AEB＝
，
∴
AB×|yE|＝，AB＝4，则yE＝﹣，
则点E（﹣，﹣）；
由△AOC∽△AEB得：
∴
；
（3）如图2，连接BF，过点F作FG⊥AC于G，
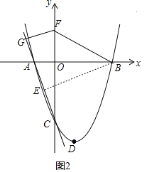
则FG＝CFsin∠FCG＝CF，
∴CF+BF＝GF+BF≥BE，
当折线段BFG与BE重合时，取得最小值，
由（2）可知∠ABE＝∠ACO
|y|＝OBtan∠ABE＝OBtan∠ACO＝3×＝，
∴当y＝﹣时，即点F（0，﹣），CF+BF有最小值；
①当点Q为直角顶点时（如图3） F（0，﹣），
∵C（0，﹣2）
∴H（0，2）设Q（1，m），过点Q作QM⊥y轴于点M．
则Rt△QHM∽Rt△FQM∴QM2＝HMFM，
∴12＝（2﹣m）（m+），
解得：m＝
，则点Q（1，）或（1，）
当点H为直角顶点时：点H（0，2），则点Q（1，2）；当点F为直角顶点时：
同理可得：点Q（1，﹣）；
综上，点Q的坐标为：（1，）或（1，）或Q（1，2）或Q（1，﹣）．
