题目内容
6. 如图,点C为线段AB上任意一点,点M是AC的中点,点N为BC的中点,如果AB=20cm,则MN=10cm.
如图,点C为线段AB上任意一点,点M是AC的中点,点N为BC的中点,如果AB=20cm,则MN=10cm.
分析 由“M为线段AC的中点,N为线段CB的中点”可知AC=2MC,CB=2CN,则有MC+NC=$\frac{1}{2}$(AC+BC);因为AB=AC+BC,MN=MC+NC,即可得解,注意不要漏掉单位.
解答 解:∵M为线段AC的中点,N为线段CB的中点,
∴AC=2MC,CB=2CN,
∵AB=AC+BC,MN=MC+NC,
∴MN=MC+NC=$\frac{1}{2}$(AC+BC)=$\frac{1}{2}$AB=10cm.
故答案为:10.
点评 本题主要考查了两点见到距离,利用中点性质转化线段之间的倍分关系,在不同情况下灵活选用它的不同表示方法,有利于解题的简洁性,此类题还要注意不要漏掉单位.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
14.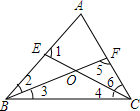 如图所示,在△ABC中,E、F分别在AB、AC上,则下列各式不能成立的是( )
如图所示,在△ABC中,E、F分别在AB、AC上,则下列各式不能成立的是( )
 如图所示,在△ABC中,E、F分别在AB、AC上,则下列各式不能成立的是( )
如图所示,在△ABC中,E、F分别在AB、AC上,则下列各式不能成立的是( )| A. | ∠BOC=∠2+∠6+∠A | B. | ∠2=∠5-∠A | C. | ∠5=∠1+∠A | D. | ∠1=∠ABC+∠4 |
16.若直线过(3,0)和(0,3)两点,则其函数表达式为( )
| A. | y=3x | B. | y=3x+3 | C. | y=x+3 | D. | y=-x+3 |
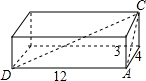 一个长方体盒子,它的长是12dm,宽是4dm,高是3dm,
一个长方体盒子,它的长是12dm,宽是4dm,高是3dm, 有理数a、b、c在数轴上的位置如图所示.化简:|a+c|-|a-b-c|-|b-a|+|b+c|.
有理数a、b、c在数轴上的位置如图所示.化简:|a+c|-|a-b-c|-|b-a|+|b+c|.