题目内容
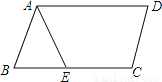
如图等腰梯形ABCD，AE是BC边上的高．已知AE=4，CE=8，则梯形ABCD的面积是（ ）
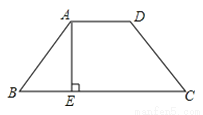
A. 16 B. 32 C. 24 D. 48
B
【解析】试题解析：过点C作CF⊥AD交AD的延长线于点F，则∠CFD=90°．
∵四边形ABCD是等腰梯形
∴AD∥BC，AB=CD，
又∵AE是BC边上的高，
∴四边形AECF是矩形．
在和中
≌（HL）．
∴梯形ABCD的面积=矩形AECF的面积=4×8=32．
故选B．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
一项工作，若甲单独完成需x小时，则甲每小时完成工作的________.若甲、乙合作 需8小时完成，则乙每小时完成工作的_______.
【解析】一项工作，若甲单独完成需x小时，则甲每小时完成工作的，
若甲、乙合作需8小时完成，则乙每小时完成工作的，
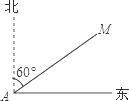
故答案为： ， . 如图，某渔船在海面上朝正东方向匀速航行，在A处观测到灯塔M在北偏东60°方向上，且AM=100海里．那么该船继续航行 海里可使渔船到达离灯塔距离最近的位置．
．
【解析】试题解析：如图，过M作东西方向的垂线，设垂足为N．
易知：∠MAN=90°=30°．
在Rt△AMN中，∵∠ANM=90°，∠MAN=30°，AM=100海里，
∴AN=AM•cos∠MAN=100×=海里．
故该船继续航行海里可使渔船到达离灯塔距离最近的位置． 如图，□ABCD中，E是BC边的中点，连接AE，F为CD边上一点，且满足∠DFA=2∠BAE．
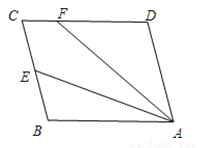
（1）若∠D=105°，∠DAF=35°．求∠FAE的度数；
（2）求证：AF=CD+CF．
（1）20°；（2）见解析
【解析】试题分析：（1）根据平行四边形的性质、平行线的性质证得；然后结合已知条件求得从而求得的度数；
（2）在AF上截取连接利用全等三角形的判定定理SAS证得 ≌，由全等三角形的对应角相等、对应边相等；然后由中点E的性质平行线的性质以及等腰三角形的判定与性质求得 最后根据线段间的和差关系证得结论．
试题解析：
（三角形内角和定理）．
∵四边... 在□ABCD中，对角线AC，BD相交于点O，AB=8cm，BC=6cm．△AOB的周长是18cm，则△AOD的周长是__________．
16cm
【解析】试题解析：
如图所示：
∵四边形ABCD是平行四边形，
的周长是18cm，AB=8cm，
的周长
故答案为：16cm． 如图，?ABCD中，BC=BD，∠C=74°，则∠ADB的度数是（ ）
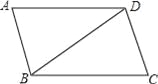
A. 16° B. 22° C. 32° D. 68°
C
【解析】试题分析：根据平行四边形的性质可知：AD∥BC，所以∠C+∠ADC=180°，再由BC=BD可得∠C=∠BDC=74°，进而可求出∠ADB=106°﹣74°=32°．
故选：C． 如图，在?ABCD中，已知AD=12cm，AB=8cm，AE平分∠BAD交BC边于点E，则CE的长等于（ ）
A．8cm B．6cm C．4cm D．2cm
C
【解析】
试题分析：【解析】
∵四边形ABCD是平行四边形，
∴BC=AD=12cm，AD∥BC，
∴∠DAE=∠BEA，
∵AE平分∠BAD，
∴∠BAE=∠DAE，
∴∠BEA=∠BAE，
∴BE=AB=8cm，
∴CE=BC﹣BE=4cm；
故答案为：C． 一个多边形中，除一个内角外，其余各内角和是120°，则这个角的度数是（ ）
A. 60° B. 80° C. 100° D. 120°
A
【解析】根据多边形的内角和公式可以知道，多边形的内角和是180°的正整数倍，所以只有A选项和120°相加是180°的正整数倍，
故选A. 光明机械厂生产一批新产品，由一班、二班合作，原计划6天完成，但是，他们合作了4天后，二班被调走了，一班对做了6天才全部做完，那么一班、二班单独做各需要几天完成？
一班单独完成需要18天，二班单独完成需要9天.
【解析】试题分析：设一班单独做需要x天完成，则一班的工作效率为，二班的工作效率为，根据工作效率工作时间=工作总量列出方程求解即可.
试题解析：设一班单独做需要x天完成，则一班的工作效率为，二班的工作效率为，
依题意得，
解得x=18，经检验知当x=18时，符合题意.∴=9，
答：一班单独完成需要18天，二班单独完成需要9...