题目内容
18. 如图,AE=CF,AD∥BC,AD=CB,求证:
如图,AE=CF,AD∥BC,AD=CB,求证:(1)△AFD≌△CEB;
(2)DF∥BE.
分析 (1)根据两直线平行内错角相等即可得出∠A=∠C,由AE=CF得到AF=CE,再根据全等三角形的判定即可判断出△ADF≌△CBE;
(2)根据△AFD≌△CEB,得到∠AFD=∠CEB,所以180°-∠AFD=180°-∠CEB,即∠DFE=∠BEF,得到DF∥BE.
解答 解:(1)∵AE=CF,
∴AE-EF=CF-EF,
即AF=CE.
∵AD∥BC,
∴∠A=∠C,
在△AFD和△CEB中,
$\left\{\begin{array}{l}{AD=CB}\\{∠A=∠C}\\{AF=CE}\end{array}\right.$,
∴△AFD≌△CEB.
(2)∵△AFD≌△CEB,
∴∠AFD=∠CEB,
∴180°-∠AFD=180°-∠CEB,
即∠DFE=∠BEF,
∴DF∥BE.
点评 本题考查了全等三角形的性质与判定,解决本题的关键是由△AFD≌△CEB,得到相等的角与边.

练习册系列答案
相关题目
3.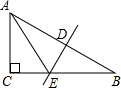 如图,在Rt△ABC中,∠C=90°,斜边AB的垂直平分线DE交AB于点D,交BC于点E,且AE平分∠BAC,下列关系式不成立的是( )
如图,在Rt△ABC中,∠C=90°,斜边AB的垂直平分线DE交AB于点D,交BC于点E,且AE平分∠BAC,下列关系式不成立的是( )
 如图,在Rt△ABC中,∠C=90°,斜边AB的垂直平分线DE交AB于点D,交BC于点E,且AE平分∠BAC,下列关系式不成立的是( )
如图,在Rt△ABC中,∠C=90°,斜边AB的垂直平分线DE交AB于点D,交BC于点E,且AE平分∠BAC,下列关系式不成立的是( )| A. | AC=2EC | B. | ∠B=∠CAE | C. | ∠DEA=∠CEA | D. | BC=3CE |
8.“直角都相等”与“相等的角是直角”是( )
| A. | 互为逆命题 | B. | 互逆定理 | C. | 公理 | D. | 假命题 |
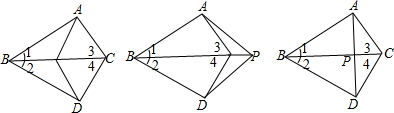
 如图,台球桌相邻两边互相垂直,若∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么打白球时,必须保证∠1的度数为60°.
如图,台球桌相邻两边互相垂直,若∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么打白球时,必须保证∠1的度数为60°.