题目内容
6.如图,在△ABC和△DBC中,∠1=∠2,∠3=∠4.P是BC上任意一点(1)求证:PA=PD;
(2)若点P改为BC延长线上任意一点,结论还成立吗?为什么?
(3)若P点是AD与BC的交点,我们还能得到什么新的结论?直接写出你的结论.
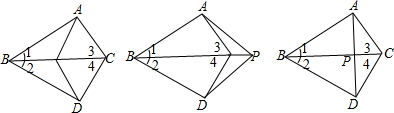
分析 (1)由已知两对角相等,且夹边为公共边相等,利用ASA得到△ABC≌△DBC,利用全等三角形对应边相等得到AB=DB,再利用SAS得到△ABP≌△DBP,利用全等三角形对应边相等即可得证;
(2)同(1)中证明相同,进而证明即可;
(3)当P点是AD与BC的交点时,可以得出AD⊥BC结论.
解答 证明:(1)在△ABC和△DBC中,
$\left\{\begin{array}{l}{∠1=∠2}\\{BC=BC}\\{∠3=∠4}\end{array}\right.$,
∴△ABC≌△DBC(ASA),
∴AB=DB,
在△ABP和△DBP中,
$\left\{\begin{array}{l}{AB=DB}\\{∠1=∠2}\\{BP=BP}\end{array}\right.$,
∴△ABP≌△DBP(SAS),
∴AP=DP;
(2)成立,理由如下:
在△ABC和△DBC中,
$\left\{\begin{array}{l}{∠1=∠2}\\{BC=BC}\\{∠3=∠4}\end{array}\right.$,
∴△ABC≌△DBC(ASA),
∴AB=DB,
在△ABP和△DBP中,
$\left\{\begin{array}{l}{AB=DB}\\{∠1=∠2}\\{BP=BP}\end{array}\right.$,
∴△ABP≌△DBP(SAS),
∴AP=DP;
(3)当P点是AD与BC的交点时,得出AD⊥BC,理由如下:
在△ABC和△DBC中,
$\left\{\begin{array}{l}{∠1=∠2}\\{BC=BC}\\{∠3=∠4}\end{array}\right.$,
∴△ABC≌△DBC(ASA),
∴AB=DB,
在△ABP和△DBP中,
$\left\{\begin{array}{l}{AB=DB}\\{∠1=∠2}\\{BP=BP}\end{array}\right.$,
∴△ABP≌△DBP(SAS),
∴∠APB=∠BPD=90°,
∴AD⊥BC.
点评 此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案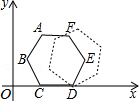 如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A、B、C、D、E、F中,最先会过点(2015,2)的是( )
如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A、B、C、D、E、F中,最先会过点(2015,2)的是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
| A. | 两边一角对应相等 | B. | 两角一边对应相等 | ||
| C. | 三边对应相等 | D. | 两边和它们的夹角对应相等 |
| A. | a=-8,b=-6 | B. | a=4,b=-3 | C. | a=3,b=8 | D. | a=8,b=-3 |
 如图,AD∥BC,AB⊥BC,CD⊥DE,DF⊥BC,CD=ED,AD=2,FC=1,则△ADE的面积为1.
如图,AD∥BC,AB⊥BC,CD⊥DE,DF⊥BC,CD=ED,AD=2,FC=1,则△ADE的面积为1. 如图,AE=CF,AD∥BC,AD=CB,求证:
如图,AE=CF,AD∥BC,AD=CB,求证: