题目内容
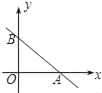
【题目】在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.
(1)求函数y=![]() x+3的坐标三角形的三条边长;
x+3的坐标三角形的三条边长;
(2)若函数y=![]() x+b(b为常数)的坐标三角形周长为16,求此三角形面积.
x+b(b为常数)的坐标三角形周长为16,求此三角形面积.
【答案】(1)函数y=![]() x+3的坐标三角形的三条边长分别为3,4,5;(2)当函数y=
x+3的坐标三角形的三条边长分别为3,4,5;(2)当函数y=![]() x+b的坐标三角形周长为16时,面积为
x+b的坐标三角形周长为16时,面积为![]() .
.
【解析】试题分析:(1)先求函数y=![]() x+3与x、y轴的交点坐标,再求三角形的三边长即可;(2)先求函数y=
x+3与x、y轴的交点坐标,再求三角形的三边长即可;(2)先求函数y=![]() x+b与x、y轴的交点坐标,再求三角形的三边长,根据三角形周长为16,列出以b为未知数的方程,解方程求的b值,在计算三角形的面积即可.
x+b与x、y轴的交点坐标,再求三角形的三边长,根据三角形周长为16,列出以b为未知数的方程,解方程求的b值,在计算三角形的面积即可.
试题解析:
(1)∵直线y=![]() x+3与x轴的交点坐标为(4,0),与y轴交点坐标为(0,3),
x+3与x轴的交点坐标为(4,0),与y轴交点坐标为(0,3),
∴函数y=![]() x+3的坐标三角形的三条边长分别为3,4,5.
x+3的坐标三角形的三条边长分别为3,4,5.
(2)直线y=![]() x+b与x轴的交点坐标为(
x+b与x轴的交点坐标为(![]() ,0),与y轴交点坐标为(0,b),
,0),与y轴交点坐标为(0,b),
AB=![]() =
=![]() =
=![]() |b|,
|b|,
当b>0时,![]() ,得b=4,
,得b=4,
此时,S△AOB=![]() =
=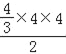 =
=![]() ,
,
∴坐标三角形面积为![]() ;
;
当b<0时,![]() ,得b=﹣4,
,得b=﹣4,
此时,S△AOB=![]() =|
=|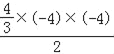 |=
|=![]() ,
,
∴坐标三角形面积为![]() .
.
综上,当函数y=![]() x+b的坐标三角形周长为16时,面积为
x+b的坐标三角形周长为16时,面积为![]() .
.

【题目】“每天锻炼一小时,健康生活一辈子”,为了选拔“阳光大课堂”领操员校组织初中三个年级推选出来的15名领操员进行比赛,成绩如下表:
成绩/分 | 7 | 8 | 9 | 10 |
人数/人 | 2 | 5 | 4 | 4 |
若任意选择一名领操员的可能性相同
(1)任意选取一名领操员,选到成绩最低领操员的概率是_________.
(2)已知获得10分的选手中,七、八、九年级分别有1人,2人,1人,学校准备从中随机选取两人领操,求恰好选到八年级两名领操员的概率.
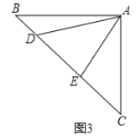
【题目】如图,在△ABC中, ![]() ,
, ![]() °,点D是线段BC上的动点,将线段AD绕点A顺时针旋转50°至
°,点D是线段BC上的动点,将线段AD绕点A顺时针旋转50°至![]() ,连接
,连接![]() .已知AB
.已知AB![]() 2cm,设BD为x cm,B
2cm,设BD为x cm,B![]() 为y cm.
为y cm.
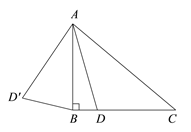
小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究,下面是小明的探究过程,请补充完整.(说明:解答中所填数值均保留一位小数)
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
|
| 0.5 | 0.7 | 1.0 | 1.5 | 2.0 | 2.3 |
| 1.7 | 1.3 | 1.1 | 0.7 | 0.9 | 1.1 |
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.

(3)结合画出的函数图象,解决问题:
线段![]() 的长度的最小值约为__________
的长度的最小值约为__________ ![]() ;
;
若![]()
![]() ,则
,则![]() 的长度x的取值范围是_____________.
的长度x的取值范围是_____________.