题目内容
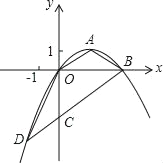
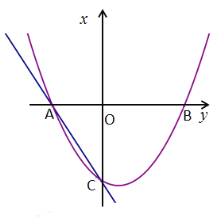
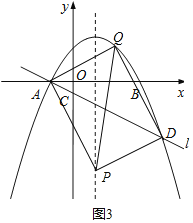
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),经过点
的左侧),经过点![]() 的直线
的直线![]() 与
与![]() 轴交于点
轴交于点![]() 与抛物线的另一个交点为,且
与抛物线的另一个交点为,且![]() .
.
(1)直接写出点![]() 的坐标,并求直线
的坐标,并求直线![]() 的函数表达式(其中
的函数表达式(其中![]() 用含
用含![]() 的式子表示);
的式子表示);
(2)点![]() 是直线
是直线![]() 上方的抛物线上的动点,若
上方的抛物线上的动点,若![]() 的面积的最大值为
的面积的最大值为![]() ,求
,求![]() 的值;
的值;
(3)设![]() 是抛物线对称轴上的一点,点
是抛物线对称轴上的一点,点![]() 在抛物线上,以点
在抛物线上,以点![]() 为顶点的四边形能否成为矩形?若能,求出点
为顶点的四边形能否成为矩形?若能,求出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
【答案】(1)A(-1,0),y=ax+a;(2)a=-![]() ;(3)能,点P(1,-
;(3)能,点P(1,-![]() )或(1,-4).
)或(1,-4).
【解析】
(1)解方程即可得到结论,再根据直线l:y=kx+b过A(-1,0),得到直线l:y=kx+k,解方程得到点D的横坐标为4,求得k=a,得到直线l的函数表达式为y=ax+a;
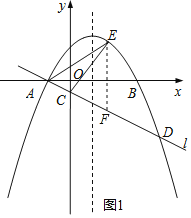
(2)过E作EF∥y轴交直线l于F,设E(x,ax2-2ax-3a),得到F(x,ax+a),求出EF=ax2-3ax-4a,根据三角形的面积公式列方程即可得到结论;
(3)令ax2-2ax-3a=ax+a,即ax2-3ax-4a=0,得到D(4,5a),设P(1,m),①若AD是矩形ADPQ的一条边,②若AD是矩形APDQ的对角线,列方程即可得到结论.
(1)当y=0时,ax2-2ax-3a=0,
解得:x1=-1,x2=3,
∴A(-1,0),B(3,0),
∵直线l:y=kx+b过A(-1,0),
∴0=-k+b,
即k=b,
∴直线l:y=kx+k,
∵抛物线与直线l交于点A,D,
∴ax2-2ax-3a=kx+k,
即ax2-(2a+k)x-3a-k=0,
∵CD=4AC,
∴点D的横坐标为4,
∴-3-![]() =-1×4,
=-1×4,
∴k=a,
∴直线l的函数表达式为y=ax+a;
(2)过E作EF∥y轴交直线l于F,设E(x,ax2-2ax-3a),
则F(x,ax+a),EF=ax2-2ax-3a-ax-a=ax2-3ax-4a,
∴S△ACE=S△AFE-S△CEF=![]() (ax2-3ax-4a)(x+1)-
(ax2-3ax-4a)(x+1)-![]() (ax2-3ax-4a)x=
(ax2-3ax-4a)x=![]() (ax2-3ax-4a)=
(ax2-3ax-4a)=![]() a(x-
a(x-![]() )2-
)2-![]() a,
a,
∴△ACE的面积的最大值=-![]() a,
a,
∵△ACE的面积的最大值为![]() ,
,
∴-![]() a=
a=![]() ,
,
解得a=-![]() ;
;
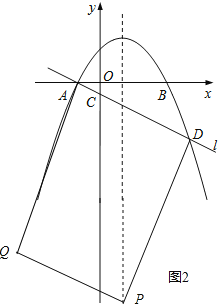
(3)以点A、D、P、Q为顶点的四边形能成为矩形,
令ax2-2ax-3a=ax+a,即ax2-3ax-4a=0,
解得:x1=-1,x2=4,
∴D(4,5a),
∵抛物线的对称轴为直线x=1,
设P(1,m),
①若AD是矩形ADPQ的一条边,
则Q(-4,21a),
m=21a+5a=26a,则P(1,26a),
∵四边形ADPQ是矩形,
∴∠ADP=90°,
∴AD2+PD2=AP2,
∴52+(5a)2+32+(26a-5a)2=22+(26a)2,
即a2=![]() ,
,
∵a<0,
∴a=-![]() ,
,
∴P(1,-![]() );
);
②若AD是矩形APDQ的对角线,
则Q(2,-3a),
m=5a-(-3a)=8a,则P(1,8a),
∵四边形APDQ是矩形,
∴∠APD=90°,
∴AP2+PD2=AD2,
∴(-1-1)2+(8a)2+(1-4)2+(8a-5a)2=52+(5a)2,
即a2=![]() ,
,
∵a<0,
∴a=-![]() ,
,
∴P(1,-4),
综上所述,点A、D、P、Q为顶点的四边形能成为矩形,点P(1,-![]() )或(1,-4).
)或(1,-4).

【题目】为了解九年级学生体育水平,学校对九年级全体学生进行了体育测试,并从甲、乙两班中各随机抽取![]() 名学生成绩(满分
名学生成绩(满分![]() 分)进行整理分析(成绩得分用
分)进行整理分析(成绩得分用![]() 表示,共分成四组:
表示,共分成四组:![]()
![]() ;
;![]()
![]() ,
,![]()
![]() )下面给出了部分信息:
)下面给出了部分信息:
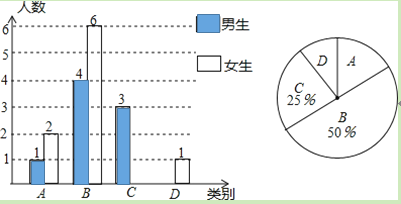
甲班![]() 名学生体育成绩:
名学生体育成绩:![]()
乙班![]() 名学生体育成绩在
名学生体育成绩在![]() 组中的数据是:
组中的数据是: ![]()
甲、乙两班被抽取学生体育成绩统计表
平均数 | 中位数 | 众数 | 方差 | |
甲班 |
|
|
|
|
乙班 |
|
|
|
|
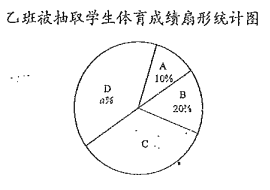
根据以上信息,解答下列问题:
![]() ,
,![]() ,
,![]() ;
;
![]() 根据以上数据,你认为 班(填“甲”或“乙”)体育水平更高,说明理由(两条理由):
根据以上数据,你认为 班(填“甲”或“乙”)体育水平更高,说明理由(两条理由):
![]() ;
;
![]() .
.
![]() 学校九年级学生共
学校九年级学生共![]() 人,估计全年级体育成绩优秀
人,估计全年级体育成绩优秀![]() 的学生人数是多少?
的学生人数是多少?