题目内容
 如图,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(-3,0),与y轴交于点C.
如图,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(-3,0),与y轴交于点C.(1)求抛物线的解析式;
(2)设抛物线的对称轴与x轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)已知抛物线过A、B两点,可将两点的坐标代入抛物线的解析式中,用待定系数法即可求出二次函数的解析式;
(2)可根据(1)的函数解析式得出抛物线的对称轴,也就得出了M点的坐标,由于C是抛物线与y轴的交点,因此C的坐标为(0,3),根据M、C的坐标可求出CM的距离.然后分三种情况进行讨论:
①当CP=PM时,P位于CM的垂直平分线上.求P点坐标关键是求P的纵坐标,过P作PQ⊥y轴于Q,如果设PM=CP=x,那么直角三角形CPQ中CP=x,OM的长,可根据M的坐标得出,CQ=3-x,因此可根据勾股定理求出x的值,P点的横坐标与M的横坐标相同,纵坐标为x,由此可得出P的坐标.
②当CM=MP时,根据CM的长即可求出P的纵坐标,也就得出了P的坐标(要注意分上下两点).
③当CM=CP时,因为C的坐标为(0,3),那么直线y=3必垂直平分PM,因此P的纵坐标是6,由此可得出P的坐标;
(2)可根据(1)的函数解析式得出抛物线的对称轴,也就得出了M点的坐标,由于C是抛物线与y轴的交点,因此C的坐标为(0,3),根据M、C的坐标可求出CM的距离.然后分三种情况进行讨论:
①当CP=PM时,P位于CM的垂直平分线上.求P点坐标关键是求P的纵坐标,过P作PQ⊥y轴于Q,如果设PM=CP=x,那么直角三角形CPQ中CP=x,OM的长,可根据M的坐标得出,CQ=3-x,因此可根据勾股定理求出x的值,P点的横坐标与M的横坐标相同,纵坐标为x,由此可得出P的坐标.
②当CM=MP时,根据CM的长即可求出P的纵坐标,也就得出了P的坐标(要注意分上下两点).
③当CM=CP时,因为C的坐标为(0,3),那么直线y=3必垂直平分PM,因此P的纵坐标是6,由此可得出P的坐标;
解答:解:(1)由题知:
解得:
∴所求抛物线解析式为: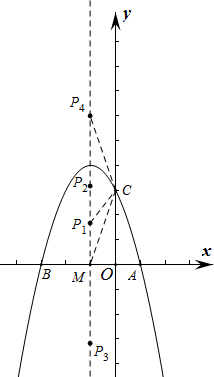 y=-x2-2x+3;
y=-x2-2x+3;
(2)∵抛物线解析式为:y=-x2-2x+3,
∴其对称轴为x=
=-1,
∴设P点坐标为(-1,a),当x=0时,y=3,
∴C(0,3),M(-1,0)
①当CP=PM时,(-1)2+(3-a)2=a2,解得a=
,
∴P点坐标为:P1(-1,
);
②当CM=PM时,(-1)2+32=a2,解得a=±
,
∴P点坐标为:P2(-1,
)或P3(-1,-
);
③当CM=CP时,由勾股定理得:(-1)2+32=(-1)2+(3-a)2,解得a=6,
∴P点坐标为:P4(-1,6)
综上所述存在符合条件的点P,其坐标为P(-1,
)或P(-1,-
)或P(-1,6)或P(-1,
);
|
解得:
|
∴所求抛物线解析式为:
 y=-x2-2x+3;
y=-x2-2x+3;(2)∵抛物线解析式为:y=-x2-2x+3,
∴其对称轴为x=
| -2 |
| 2 |
∴设P点坐标为(-1,a),当x=0时,y=3,
∴C(0,3),M(-1,0)
①当CP=PM时,(-1)2+(3-a)2=a2,解得a=
| 5 |
| 3 |
∴P点坐标为:P1(-1,
| 5 |
| 3 |
②当CM=PM时,(-1)2+32=a2,解得a=±
| 10 |
∴P点坐标为:P2(-1,
| 10 |
| 10 |
③当CM=CP时,由勾股定理得:(-1)2+32=(-1)2+(3-a)2,解得a=6,
∴P点坐标为:P4(-1,6)
综上所述存在符合条件的点P,其坐标为P(-1,
| 10 |
| 10 |
| 5 |
| 3 |
点评:本题主要考查了二次函数的综合知识,要注意的是(2)中,不确定等腰三角形哪条边是底边的情况下,要分类进行求解,不要漏解.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
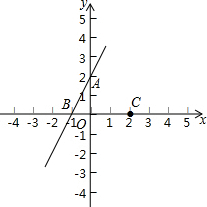 如图,在平面直角坐标系中,点A、B、C的坐标分别为(0,2)、(-1,0)、(2,0).
如图,在平面直角坐标系中,点A、B、C的坐标分别为(0,2)、(-1,0)、(2,0). 如图,梯形ABCD的两条对角线交于点E,图中面积相等的三角形共有
如图,梯形ABCD的两条对角线交于点E,图中面积相等的三角形共有