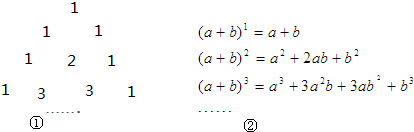题目内容
14．数据a，a+1，a+2，a+3，a-3，a-2，a-1的平均数为a，中位数是a．分析 根据平均数和中位数的概念求解．
解答 解：这组数据按从小到大的顺序排列为：a-3，a-2，a-1，a，a+1，a+2，a+3，
则平均数为：$\frac{a-3+a-2+a-1+a+a+1+a+2+a+3}{7}$=a，
中位数为：a．
故答案为：a，a．
点评 本题考查了中位数和平均数的知识，将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数；如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数；平均数是指在一组数据中所有数据之和再除以数据的个数．
练习册系列答案
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案
相关题目
4．
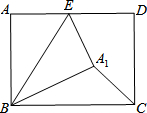如图，在矩形ABCD中，AB=3，BC=4，点E是AD上一个动点，把△BAE沿BE向矩形内部折叠，当点A的对应点A1恰落在∠BCD的平分线上时，CA1的长为（ ）
如图，在矩形ABCD中，AB=3，BC=4，点E是AD上一个动点，把△BAE沿BE向矩形内部折叠，当点A的对应点A1恰落在∠BCD的平分线上时，CA1的长为（ ）| A． | 2$\sqrt{2}$ | B． | $\sqrt{3}±1$ | C． | 2$\sqrt{2}$±1 | D． | $\sqrt{6}±\sqrt{2}$ |
2．下列四个几何体中，从正面看到的图形与从左面的图形相同的几何体有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
9．已知二次函数y=a（x+1）2+b有最大值0.1，则a与b的大小关系为（ ）
| A． | a＞b | B． | a＜b | C． | a=b | D． | 不能确定 |
如图，E，F是平行四边形ABCD的对角线AC上的点，CE=AF．求证：
4．一列数a1，a2，a3，…，其中a1=$\frac{1}{2}$，an=$\frac{1}{1+{a}_{n-1}}$（n为不小于2的整数），则a9=（ ）
| A． | $\frac{34}{55}$ | B． | $\frac{21}{34}$ | C． | $\frac{55}{89}$ | D． | $\frac{89}{144}$ |