题目内容
4.一列数a1,a2,a3,…,其中a1=$\frac{1}{2}$,an=$\frac{1}{1+{a}_{n-1}}$(n为不小于2的整数),则a9=( )| A. | $\frac{34}{55}$ | B. | $\frac{21}{34}$ | C. | $\frac{55}{89}$ | D. | $\frac{89}{144}$ |
分析 先根据给出的公式和已知进行计算,然后根据计算的结果总结规律:an的分子、分母分别是an-1的分母、分子与分母的和.
解答 解:a2=$\frac{1}{1+\frac{1}{2}}$=$\frac{2}{3}$
a3=$\frac{1}{1+\frac{2}{3}}$=$\frac{3}{5}$
可以发现an的分子、分母分别是an-1的分母、分子与分母的和
…
a9=$\frac{55}{89}$
故选:C.
点评 本题是根据计算结果,总结数字的变化规律,解题的关键是通过前几项的计算结果,发现后一项的分子、分母与前一项的分子、分母之间的关系,根据关系进行解答.

练习册系列答案
相关题目
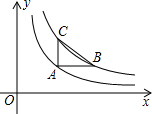 如图,已知点A在反比例函数y=$\frac{2}{x}$的图象上,点B,C分别在反比例函数y=$\frac{4}{x}$的图象上,且AB∥x轴,AC∥y轴,若AB=2AC,则点A的坐标为(2,1).
如图,已知点A在反比例函数y=$\frac{2}{x}$的图象上,点B,C分别在反比例函数y=$\frac{4}{x}$的图象上,且AB∥x轴,AC∥y轴,若AB=2AC,则点A的坐标为(2,1).