题目内容
19. 如图,E,F是平行四边形ABCD的对角线AC上的点,CE=AF.求证:
如图,E,F是平行四边形ABCD的对角线AC上的点,CE=AF.求证:(1)BE=DF;
(2)BE∥DF.
分析 (1)由AF=CE可得AE=CF,再结合平行四边形的性质证明△ABE≌△CDF,从而得出BE=DF;
(2)利用平行线的判定方法得出即可.
解答 证明:(1)∵AF=CE,
∴AF-EF=CE-EF.
∴AE=CF.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∴∠BAE=∠DCF.
在△ABE和△CDF中
∵$\left\{\begin{array}{l}{AE=CF}\\{∠BAE=∠DCF}\\{AB=CD}\end{array}\right.$,
∴△ABE≌△CDF(SAS).
∴BE=DF,
(2)∵△ABE≌△CDF(SAS),
∴∠BAE=∠DCF,
∴BE∥DF.
点评 此题主要考查了全等三角形的性质与判定、平行四边形的性质,首先利用平行四边形的性质构造全等条件,然后利用全等三角形的性质解决问题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
9.已知y=$\sqrt{2x-5}$+$\sqrt{5-2x}$-3,则2xy的值为( )
| A. | $\frac{15}{2}$ | B. | 15 | C. | -$\frac{15}{2}$ | D. | -15 |
8.下列计算正确的是( )
| A. | -(-a)4÷a2=-a2 | B. | (2a+3b)(2a-3b)=2a2-3b2 | ||
| C. | (xy)-1($\frac{1}{2}$xy)2=$\frac{1}{4}$xy2 | D. | 3ab-2ab=1 |
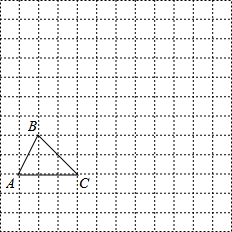 如图,在边长为1个长度单位的小正方形组成的网格中,给出了△ABC(顶点是网格线的交点).
如图,在边长为1个长度单位的小正方形组成的网格中,给出了△ABC(顶点是网格线的交点).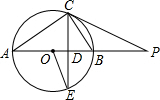 如图,AB是⊙O的直径,点P在AB的延长线上,弦CE交AB于点D.连结OE、AC,已知∠POE=2∠CAB,∠P=∠E.
如图,AB是⊙O的直径,点P在AB的延长线上,弦CE交AB于点D.连结OE、AC,已知∠POE=2∠CAB,∠P=∠E.