题目内容
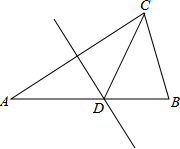 如图,在△ABC中,AB=AC,∠A=36°,DE是AC的垂直平分线.
如图,在△ABC中,AB=AC,∠A=36°,DE是AC的垂直平分线.(1)求证:△BCD是等腰三角形;
(2)△BCD的周长是a,BC=b,求△ACD的周长(用含a,b的代数式表示)
考点:线段垂直平分线的性质,等腰三角形的判定与性质
专题:
分析:(1)先由AB=AC,∠A=36°,可求∠B=∠ACB=
=72°,然后由DE是AC的垂直平分线,可得AD=DC,进而可得∠ACD=∠A=36°,然后根据外角的性质可求:∠CDB=∠ACD+∠A=72°,根据等角对等边可得:CD=CB,进而可证△BCD是等腰三角形;
(2)由(1)知:AD=CD=CB=b,由△BCD的周长是a,可得AB=a-b,由AB=AC,可得AC=a-b,进而得到△ACD的周长=AC+AD+CD=a-b+b+b=a+b.
| 180°-∠A |
| 2 |
(2)由(1)知:AD=CD=CB=b,由△BCD的周长是a,可得AB=a-b,由AB=AC,可得AC=a-b,进而得到△ACD的周长=AC+AD+CD=a-b+b+b=a+b.
解答:(1)证明:∵AB=AC,∠A=36°,
∴∠B=∠ACB=
=72°,
∵DE是AC的垂直平分线,
∴AD=DC,
∴∠ACD=∠A=36°,
∵∠CDB是△ADC的外角,
∴∠CDB=∠ACD+∠A=72°,
∴∠B=∠CDB,
∴CB=CD,
∴△BCD是等腰三角形;
(2)解:∵AD=CD=CB=b,△BCD的周长是a,
∴AB=a-b,
∵AB=AC,
∴AC=a-b,
∴△ACD的周长=AC+AD+CD=a-b+b+b=a+b.
∴∠B=∠ACB=
| 180°-∠A |
| 2 |
∵DE是AC的垂直平分线,
∴AD=DC,
∴∠ACD=∠A=36°,
∵∠CDB是△ADC的外角,
∴∠CDB=∠ACD+∠A=72°,
∴∠B=∠CDB,
∴CB=CD,
∴△BCD是等腰三角形;
(2)解:∵AD=CD=CB=b,△BCD的周长是a,
∴AB=a-b,
∵AB=AC,
∴AC=a-b,
∴△ACD的周长=AC+AD+CD=a-b+b+b=a+b.
点评:此题考查了等腰三角形的性质,线段垂直平分线的性质以及三角形内角和定理等知识.此题综合性较强,但难度不大,解题的关键是注意数形结合思想的应用,注意等腰三角形的性质与等量代换.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在同一直角坐标系中,函数y=2x与y=-
的图象大致是( )
| 1 |
| x |
A、 |
B、 |
C、 |
D、 |
 如图,△ABC的顶点A、B、C均在⊙O上,∠ABC+∠AOC=90°,则∠AOC等于( )
如图,△ABC的顶点A、B、C均在⊙O上,∠ABC+∠AOC=90°,则∠AOC等于( )| A、30° | B、45° |
| C、60° | D、75° |
 如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直线,点P是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直线,点P是⊙O的直径,点P是CD延长线上的一点,且AP=AC. 如图,在△ABC中,点D、E、F分别在AB、AC、BC边上,DE∥BC,DF∥AC,AF与DE交于点G,BE与DF交于点H,求证:GH∥AB.
如图,在△ABC中,点D、E、F分别在AB、AC、BC边上,DE∥BC,DF∥AC,AF与DE交于点G,BE与DF交于点H,求证:GH∥AB. 如图,在Rt△ABC中,∠C=90°,a、b、c分别表示∠A,∠B,∠C的对边.
如图,在Rt△ABC中,∠C=90°,a、b、c分别表示∠A,∠B,∠C的对边. 如图,在△ABC中,∠C=90°,BD平分∠CBA交AC于点D,若AB=6,CD=2,则△ADB的面积为
如图,在△ABC中,∠C=90°,BD平分∠CBA交AC于点D,若AB=6,CD=2,则△ADB的面积为 如图,在两个同心圆中,两圆半径分别为2和1,∠AOB=120°,求阴影部分的面积.
如图,在两个同心圆中,两圆半径分别为2和1,∠AOB=120°,求阴影部分的面积.