题目内容
如图，在△ABC中，∠C=90°，BD平分∠CBA交AC于点D，若AB=6，CD=2，则△ADB的面积为考点：角平分线的性质
专题：
分析：过D作DE⊥AB于点E，由角平分线的性质可得DE=DC，再由三角形的面积公式可求得答案．
解答：
解：如图，过D作DE⊥AB于点E，
∵BD平分∠ABC，DC⊥BC，
∴DE=CD=2，
∴S△ABD=
AB•DE=
×6×2=6，
故答案为：6．
解：如图，过D作DE⊥AB于点E，∵BD平分∠ABC，DC⊥BC，
∴DE=CD=2，
∴S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为：6．
点评：本题主要考查角平分线的性质，掌握角平分线上的点到角两边的距离相等是解题的关键．
练习册系列答案
相关题目
下列结论错误的是（ ）
| A、圆是轴对称图形 |
| B、圆是中心对称图形 |
| C、半圆不是弧 |
| D、同圆中，等弧所对的圆心角相等 |
如图，AB∥CD∥EF∥GH，AC：CE：EG=2：3：4，BD=3，则BH=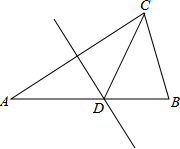
如图，在△ABC中，AB=AC，∠A=36°，DE是AC的垂直平分线．
如图，利用方格纸上的格点画图，并标上相应的字母．
．小明翻看了书后的答案，此方程的解是y=-