题目内容
 如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直线,点P是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直线,点P是⊙O的直径,点P是CD延长线上的一点,且AP=AC.(1)求证:PA是⊙O的切线;
(2)若PA=
| 3 |
考点:切线的判定
专题:
分析:(1)连接OA、AD,可求得∠ACP=∠APC=30°,可证明△AOD为等边三角形,可求得∠PAO=90°,可证明PA为⊙O的切线;
(2)结合(1)可得到OP=2AO,在Rt△APO中由勾股定理可求得AO,可求得直径.
(2)结合(1)可得到OP=2AO,在Rt△APO中由勾股定理可求得AO,可求得直径.
解答:(1)证明:
连接OA、AD,如图,
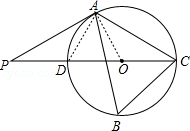
∵CD为⊙O的直径,
∴∠DAC=90°,
又∠ADC=∠B=60°,
∴∠ACD=30°,
又PA=AC,OA=OD,
∴△ADO为等边三角形,
∴∠P=30°,∠ADO=∠DAO=60°,
∴∠PAD=30°,
∴∠PAD+∠DAO=90°,
∴OA⊥PA,
∴PA为⊙O的切线;
(2)解:
由(1)可知△APO为直角三角形,且∠P=30°,
∴PO=2AO,且PA=
,
由勾股定理可得PO2=AO2+PA2,可解得AO=1,
∴CD=2,即⊙O的直径为2.
连接OA、AD,如图,

∵CD为⊙O的直径,
∴∠DAC=90°,
又∠ADC=∠B=60°,
∴∠ACD=30°,
又PA=AC,OA=OD,
∴△ADO为等边三角形,
∴∠P=30°,∠ADO=∠DAO=60°,
∴∠PAD=30°,
∴∠PAD+∠DAO=90°,
∴OA⊥PA,
∴PA为⊙O的切线;
(2)解:
由(1)可知△APO为直角三角形,且∠P=30°,
∴PO=2AO,且PA=
| 3 |
由勾股定理可得PO2=AO2+PA2,可解得AO=1,
∴CD=2,即⊙O的直径为2.
点评:本题主要考查切线的判定和性质,掌握切线的证明方法是解题的关键,即有切点时连接圆心和切点证明垂直,没有切点时,作垂直证明距离等于半径.注意这类问题的常用辅助线的作法.

练习册系列答案
相关题目
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对于下列结论:①b2-4ac>0;②a+b+c<0;③abc<0;④8a+c>0;⑤方程ax2+bx+c=0的根是x1=-1,x2=3,其中正确结论的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对于下列结论:①b2-4ac>0;②a+b+c<0;③abc<0;④8a+c>0;⑤方程ax2+bx+c=0的根是x1=-1,x2=3,其中正确结论的个数是( )| A、5 | B、4 | C、3 | D、2 |
如果要在一条直线上得到6条不同的线段,那么在这条直线上应选( )
| A、3个不同点 |
| B、4个不同点 |
| C、5个不同点 |
| D、6个不同点 |
如图给出的分别有射线、直线、线段,其中能相交的图形有( )

| A、①②③④ | B、① |
| C、②③④ | D、①③ |
 如图,四边形OABC各个顶点的坐标分别是O(0,0),A(3,0),B(5,2),C(2,3).求这个四边形的面积.
如图,四边形OABC各个顶点的坐标分别是O(0,0),A(3,0),B(5,2),C(2,3).求这个四边形的面积. 如图,在△ABC中,AB=AC,∠A=36°,DE是AC的垂直平分线.
如图,在△ABC中,AB=AC,∠A=36°,DE是AC的垂直平分线.