题目内容
11.(1)已知a-b=3,b+c=-5,求代数式ac-bc+a2-ab的值;(2)若a=(2$\sqrt{3}$+$\sqrt{6}$),b=(2$\sqrt{3}$-$\sqrt{6}$),求a2b+ab2的值.
分析 (1)首先将原式分解因式,进而将已知代入求出答案;
(2)直接将原式分解因式,进而将已知代入求出答案.
解答 解:(1)由a-b=3,b+c=-5,得a+c=-2,
ac-bc+a2-ab=c(a-b)+a(a-b),
=(a-b)(c+a)
=3×(-2)
=-6;
(2)由a=2$\sqrt{3}$+$\sqrt{6}$,b=2$\sqrt{3}$-$\sqrt{6}$得,
ab=(2$\sqrt{3}$+$\sqrt{6}$)×(2$\sqrt{3}$-$\sqrt{6}$)=6,
a+b=4$\sqrt{3}$
a 2b+ab2=ab(a+b)
=6×4$\sqrt{3}$
=24$\sqrt{3}$.
点评 此题主要考查了因式分解的应用,正确分解因式是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.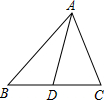 如图,在△ABC中,AC=5,中线AD=7,则AB边的取值范围是( )
如图,在△ABC中,AC=5,中线AD=7,则AB边的取值范围是( )
 如图,在△ABC中,AC=5,中线AD=7,则AB边的取值范围是( )
如图,在△ABC中,AC=5,中线AD=7,则AB边的取值范围是( )| A. | 1<AB<29 | B. | 4<AB<24 | C. | 5<AB<19 | D. | 9<AB<19 |
20.下列各组数中,互为相反数的是( )
| A. | -3与+(-3) | B. | -(-3)与+|-3| | C. | +3 与-|+3| | D. | +(-3)与-|-3| |
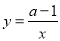 上,则a的值为__________.
上,则a的值为__________. 如图所示,在四边形ABCD中,AB∥CD,AD=BC,∠A=∠B=90°,E是AB上一点,且DE=DC,过点C作CF⊥DE,垂足为点F.
如图所示,在四边形ABCD中,AB∥CD,AD=BC,∠A=∠B=90°,E是AB上一点,且DE=DC,过点C作CF⊥DE,垂足为点F.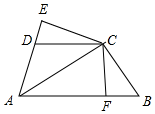 如图所示,AB∥DC,DC=CB,CE⊥AD,交AD的延长线于E,CF⊥AB垂足为F,∠DAB=∠B,求证:AC平分∠DAB.
如图所示,AB∥DC,DC=CB,CE⊥AD,交AD的延长线于E,CF⊥AB垂足为F,∠DAB=∠B,求证:AC平分∠DAB.