题目内容
6.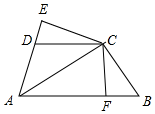 如图所示,AB∥DC,DC=CB,CE⊥AD,交AD的延长线于E,CF⊥AB垂足为F,∠DAB=∠B,求证:AC平分∠DAB.
如图所示,AB∥DC,DC=CB,CE⊥AD,交AD的延长线于E,CF⊥AB垂足为F,∠DAB=∠B,求证:AC平分∠DAB.
分析 欲证明AC平分∠DAB,只要证明△CED≌△CFB,推出CE=CF,即可解决问题.
解答 证明:如图,
∵∴CF⊥AB,CE⊥AE,
∴∠CED=∠CFB=90°,
∵CD∥AB,
∴∠EDC=∠DAB=∠B,
在△CED和△CFB中,
$\left\{\begin{array}{l}{∠CED=∠CFB}\\{∠CDE=∠B}\\{CD=CB}\end{array}\right.$,
∴△CED≌△CFB,
∴CE=CF,∵CF⊥AB,CE⊥AE,
∴AC是∠DAB的角平分线.
点评 本题考查全等三角形的判定和性质、角平分线的判定定理、平行线的性质等知识,解题的关键是熟练掌握角平分线的判定定理的应用,属于中考常考题型.

练习册系列答案
相关题目
某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:
组号 | 分组 | 频数 |
一 | 6≤m<7 | 2 |
二 | 7≤m<8 | 7 |
三 | 8≤m<9 | a |
四 | 9≤m≤10 | 2 |
(1)求a的值;
(2)若用扇形图来描述,求分数在8≤m<9内所对应的扇形图的圆心角大小;
(3)将在第一组内的两名选手记为:A1、A2,在第四组内的两名选手记为:B1、B2,从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率(用树状图或列表法列出所有可能结果).
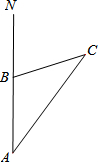 如图,上午9时,一条船从A处出发,以20海里/时的速度向正北航行,12时到达B处,测得∠NAC=36°,∠ABC=108°,求从B处到灯塔C的距离.
如图,上午9时,一条船从A处出发,以20海里/时的速度向正北航行,12时到达B处,测得∠NAC=36°,∠ABC=108°,求从B处到灯塔C的距离.