题目内容
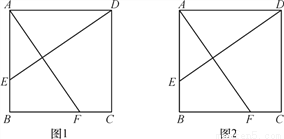
如图1,在正方形ABCD中,点E,F分别在AB,BC上,且AE=BF.
(1)试探索线段AF,DE的数量关系,写出你的结论并说明理由;
(2)连接EF,DF,分别取AE,EF,FD,DA的中点H,I,J,K,则四边形HIJK是什么特殊四边形?请在图2中补全图形,并说明理由.
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
题目内容
如图1,在正方形ABCD中,点E,F分别在AB,BC上,且AE=BF.
(1)试探索线段AF,DE的数量关系,写出你的结论并说明理由;
(2)连接EF,DF,分别取AE,EF,FD,DA的中点H,I,J,K,则四边形HIJK是什么特殊四边形?请在图2中补全图形,并说明理由.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案