题目内容
18.已知关于x的不等式组$\left\{\begin{array}{l}{x+a>0}\\{2-x>0}\end{array}\right.$的整数解共有3个,则a的取值范围是1<a≤2.分析 首先解不等式组,利用a表示出不等式组的解集,然后根据不等式组有3个整数解,即可确定整数解,进而求得a的范围.
解答 解:$\left\{\begin{array}{l}{x+a>0…①}\\{2-x>0…②}\end{array}\right.$,
解①得x>-a,
解②得x<2.
则不等式组的解集是-a<x<2.
∵不等式组$\left\{\begin{array}{l}{x+a>0}\\{2-x>0}\end{array}\right.$的整数解共有3个,
∴整数解是1,0,-1.
则-2≤-a<-1.
解得:1<a≤2.
故答案是:1<a≤2.
点评 本题考查了不等式组的整数解,求不等式组的解集应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
相关题目
6.已知在一次函数y=-2x+b的图象上有三点(-2,y1),(-1,y2)(1,y3),则y1,y2,y3的大小关系( )
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y3>y2>y1 | D. | y3>y1>y2 |
13.如果一个等腰梯形两底的差等于一腰长,那么它的腰与下底的夹角的度数是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
3.用中位数去估计总体时,其优越性是( )
| A. | 运算简便 | B. | 不受个别数据较大或较小的影响 | ||
| C. | 不受较小数据的影响 | D. | 不受较大数据的影响 |
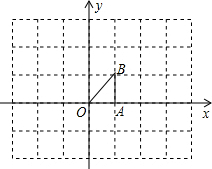 如图,在直角坐标系中的△OAB,其中A(1,0),B(1,1).
如图,在直角坐标系中的△OAB,其中A(1,0),B(1,1).