Question

【题目】已知抛物线经过点，与轴交于两点

求抛物线的解析式；

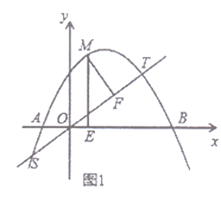
如图1，直线交抛物线于两点，为抛物线上之间的动点，过点作轴于点于点，求的最大值；

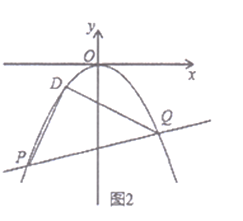
如图2，平移抛物线的顶点到原点得抛物线，直线交抛物线于、两点，在抛物线上存在一个定点，使，求点的坐标．

Answer 1

【答案】（1）；（2）； （3） ．

【解析】

（1）利用待定系数法即可得出结论；

（2）先确定出ME，MF与t的关系，最后建立ME+MF与t的函数关系式，即可得出结论；

（3）先求出x2+2kx﹣4k﹣8＝0，进而得出x1+x2＝﹣2k，x1x2＝﹣4k﹣8，而DEDF＝PEQF，得出（a﹣x1）（x2﹣a）＝（b﹣y1）（b﹣y2），借助，，，即可得出（a﹣x1）（x2﹣a）＝（a+x1）（a+x2）（x1﹣a）（x2﹣a），即可得出结论．

解：（1）∵抛物线C：y＝ax2﹣2ax+c经过点C（1，2），与x轴交于A（﹣1，0）、B两点

解得：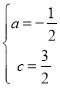

抛物线C的解析式为

（2）如图1，设直线交于点，

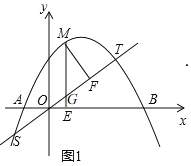
设，

则，

，，

，

，

，

由题意可知: -1<t<2

，

当时，ME+MF的最大值是．

（3）由题意可知，抛物线的解析式为；

如图2，过D作EF∥x轴，作PE⊥E'F于E，QF⊥EF于F，

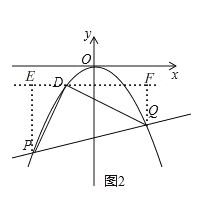
设，

联立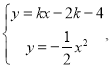

得

由∽，得，

，

，，，

，

∴，

即：

∴，

∴

∴，

即：

为任意数，