Question

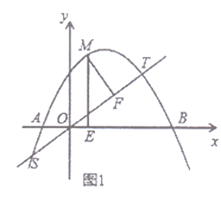
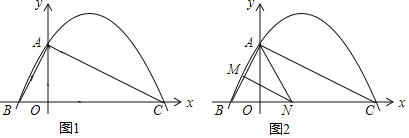
【题目】如图，已知直线分别交轴、轴于点、，抛物线过，两点，点是线段上一动点，过点作轴于点，交抛物线于点．

（1）若抛物线的顶点的坐标为，其对称轴交于点，

①求抛物线的解析式；

②是否存在点，使四边形为菱形？并说明理由；

（2）当点的横坐标为1时，是否存在这样的抛物线，使得以、、为顶点的三角形与相似？若存在，求出满足条件的抛物线的解析式：若不存在，请说明理由．

Answer 1

【答案】（1）①或写成y②不存在．（2）存在．

满足条件的抛物线的解析式为或．

【解析】

（1）①利用顶点M将抛物线设为顶点式，代入点A的坐标即可求得；

（1）②根据PM∥MN可知，PD=MN时，四边形MNPD是平行四边形.在求m值来确定菱形；

（2）先求出PB的长，然后设抛物线为，代入A的坐标可得出a与b的关系.在利用∠DPB=∠OBA讨论可求得

（1）①∵抛物线的顶点的坐标为

∴设

抛物线过点A，根据一次函数可得A(2，0)代入解析式得

a=－2

∴抛物线解析式为

②不存在．

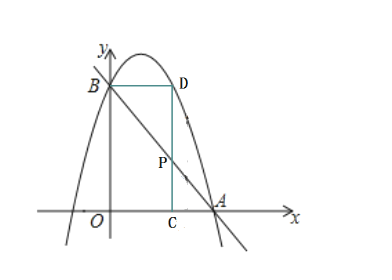
理由如下：（如图）

，

设点坐标为(m，－2m+4)，则，

∴PD=－(－2m+4)=，

∵，

当时，四边形为平行四边形，即，解得（舍去），，此时点坐标为，

∵，

∴，∴平行四边形不为菱形，

∴不存在点，使四边形为菱形；

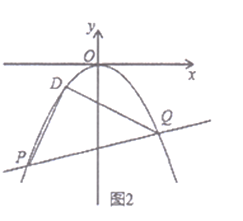
（2）存在．

如图，，，则，

当时，y=－2x+4=2，则，

∴PB=，

设抛物线的解析式，

把代入得4a+2b+4=0，解得b=－2a－2，

∴抛物线的解析式为，

当时，，则D(1，2－a)，

∴PD=－a，

∵，∴∠DPB=∠OBA，

∴当时，，即，解得，此时抛物线解析式为；

当时，，即，解得，此时抛物线解析式为y=；

综上所述，满足条件的抛物线的解析式为或y=．