题目内容
10.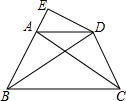 四边形ABCD是等腰梯形,AB=CD,AD∥BC,DE∥CA交BA的延长线于点E,求证:ED•AB=EA•BD.
四边形ABCD是等腰梯形,AB=CD,AD∥BC,DE∥CA交BA的延长线于点E,求证:ED•AB=EA•BD.
分析 由平行线的性质得出∠BAC=∠AED,∠EDA=∠CAD,∠CAD=∠ACB,得出∠EDA=∠ACB,证出△AED∽△BAC,得出对应边成比例$\frac{ED}{EA}=\frac{AC}{AB}$,再由等腰梯形的性质得出BD=AC,得出$\frac{ED}{EA}=\frac{BD}{AB}$,即可得出结论.
解答 证明:∵DE∥CA,AD∥BC,
∴∠BAC=∠AED,∠EDA=∠CAD,∠CAD=∠ACB,
∴∠EDA=∠ACB,
∴△AED∽△BAC,
∴$\frac{ED}{EA}=\frac{AC}{AB}$,
∵四边形ABCD是等腰梯形,AB=CD,
∴BD=AC,
∴$\frac{ED}{EA}=\frac{BD}{AB}$,
∴ED•AB=EA•BD.
点评 本题考查了相似三角形的判定与性质、等腰梯形的性质;熟练掌握等腰梯形的性质,证明三角形相似是解决问题的关键.

练习册系列答案
相关题目
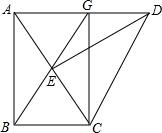 如图,在Rt△ABC中,∠ABC=90°,将Rt△ABC绕点C沿顺时针方向旋转60°得到△DEC,点E在AC上,连接AD,BE,并延长BE交AD于G,连接CG.问:四边形ABCG是什么特殊的四边形?为什么?
如图,在Rt△ABC中,∠ABC=90°,将Rt△ABC绕点C沿顺时针方向旋转60°得到△DEC,点E在AC上,连接AD,BE,并延长BE交AD于G,连接CG.问:四边形ABCG是什么特殊的四边形?为什么?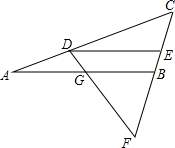 如图,已知DE∥GB.且$\frac{AD}{DG}$=$\frac{AC}{BC}$,求证:△DEF是等腰三角形.
如图,已知DE∥GB.且$\frac{AD}{DG}$=$\frac{AC}{BC}$,求证:△DEF是等腰三角形. 尺规作图:(要求保留作图痕迹,不要求写出作法)
尺规作图:(要求保留作图痕迹,不要求写出作法)