题目内容
在直线l上顺次取A,B,C,D四点,并且使AB:BC:CD=2:3:4,如果AB中点M与CD中点N的距离是12cm,那么CD的长是( )
| A、4cm | B、6cm |
| C、8cm | D、24cm |
考点:两点间的距离
专题:
分析:根据题意画出图形,设AB=2x,则BC=3x,CD=4x,再根据点M、N分别是线段AB,CD的中点可知BM=x,CN=2x,再由MN=12cm求出x的值,进而可得出结论.
解答:解:如图所示,
∵AB:BC:CD=2:3:4,
∴设AB=2x,则BC=3x,CD=4x,
∵点M、N分别是线段AB,CD的中点,
∴BM=x,CN=2x,
∴MN=BM+BC+CN=x+3x+2x=12,解得x=2,
∴CD=4x=8cm.
故选C.
∵AB:BC:CD=2:3:4,

∴设AB=2x,则BC=3x,CD=4x,
∵点M、N分别是线段AB,CD的中点,
∴BM=x,CN=2x,
∴MN=BM+BC+CN=x+3x+2x=12,解得x=2,
∴CD=4x=8cm.
故选C.
点评:本题考查的是两点间的距离,熟知各线段之间的和、差及倍数关系是解答此题的关键.

练习册系列答案
相关题目
依依买了7本数学书和2本语文书共花了100元;菲菲买了4本语文书和2本数学书共花了80元.则买3本数学书要花( )元.
| A、30 | B、20 | C、15 | D、45 |
已知a与b互为相反数,且b≠0,下列各式不成立的是( )
| A、a+b=0 | ||
| B、a2=b2 | ||
| C、|a|=-|b| | ||
D、
|
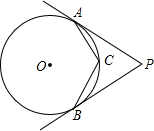 如图,PA,PB分别与⊙O相切于A,B两点,点C是劣弧AB上一动点(不与A,B重合),∠P=70°,则∠C=( )
如图,PA,PB分别与⊙O相切于A,B两点,点C是劣弧AB上一动点(不与A,B重合),∠P=70°,则∠C=( )| A、110° | B、115° |
| C、120° | D、125° |
 已知:如图,AB:BC:CD=1:3:2,M为AB的中点,N为CD的中点,且MN=9,求AD的长.
已知:如图,AB:BC:CD=1:3:2,M为AB的中点,N为CD的中点,且MN=9,求AD的长. 点A在DE上,AC=CE,∠1=∠2=∠3,求证:AB=DE.
点A在DE上,AC=CE,∠1=∠2=∠3,求证:AB=DE. 如图,线段AB=10cm,C是线段AB上任意一点,M,N分别是AC,BC的中点,“AM=4cm,BN的长为
如图,线段AB=10cm,C是线段AB上任意一点,M,N分别是AC,BC的中点,“AM=4cm,BN的长为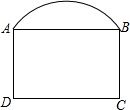 如图,工厂大门由弧线AB和矩形ABCD组成,
如图,工厂大门由弧线AB和矩形ABCD组成,
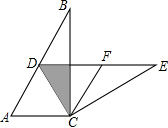 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按照顺时针方向旋转m度后得到△DEC,点D刚好落在AB边上.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按照顺时针方向旋转m度后得到△DEC,点D刚好落在AB边上.