题目内容
19.在Rt△ABC中,∠C=90°.(1)AC=24,AB=25,求tanA和tanB;
(2)BC=3,tanA=0.6,求AC和AB.
分析 (1)先利用勾股定理计算出BC,然后根据正切的定义求解;
(2)先利用∠A的正切求出AC的长,然后利用勾股定理计算AB的长.
解答 解:(1)BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{2{5}^{2}-2{4}^{2}}$=7,
所以tanA=$\frac{BC}{AC}$=$\frac{7}{24}$,
tanB=$\frac{AC}{BC}$=$\frac{24}{7}$;
(2)∵tanA=$\frac{BC}{AC}$,
∴AC=$\frac{3}{0.6}$=5,
∴AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=$\sqrt{{3}^{2}+{5}^{2}}$=$\sqrt{34}$.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.解决本题的关键是灵活应用勾股定理和三角函数的定义进行计算.

练习册系列答案
相关题目
9.若a0、b0都是单位向量,则有( )
| A. | a0=b0 | B. | a0=-b0 | C. | |a0|=|b0| | D. | a0=±b0 |
4.已知扇形的圆心角为120°,半径为6cm的圆,则扇形的弧长为( )
| A. | 3cm | B. | 3πcm | C. | 4cm | D. | 4πcm |
9.下列计算正确的是( )
| A. | ($\frac{2{a}^{-3}b}{-{c}^{3}}$)2=$\frac{4{a}^{9}b}{{c}^{5}}$ | B. | ($\frac{2x-y}{-5{a}^{2}}$)2=$\frac{4{x}^{2}-{y}^{2}}{25{a}^{4}}$ | ||
| C. | (3xny-n)-m=$\frac{{y}^{mn}}{{3}^{m}x^{mn}}$ | D. | (-$\frac{{b}^{2}}{a}$)2n=-$\frac{{b}^{2+2n}}{{a}^{n}}$ |
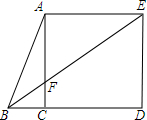 如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,以AC为边向三角形外作正方形ACDE,连接BE交AC于F.若BF=$\sqrt{3}$cm,则EF=3.
如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,以AC为边向三角形外作正方形ACDE,连接BE交AC于F.若BF=$\sqrt{3}$cm,则EF=3.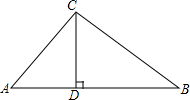 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,CD=8,AC=10.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,CD=8,AC=10.